
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用微信交流”的态度与人的年龄有关:
的把握认为“使用微信交流”的态度与人的年龄有关:
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为
的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据如下:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考公式:![]() ,
,![]() .
.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】为了了解我国各景点在大众中的熟知度,随机对![]() ~
~![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
人,回答问题“我国的“五岳”指的是哪五座名山?”统计结果如下图表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组[ | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
![]()
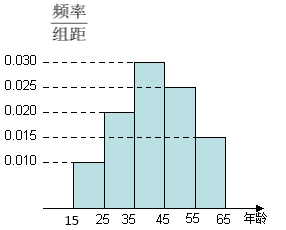
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组各抽取多少人;
组每组各抽取多少人;
(3)在(2)的条件下抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求所抽取的人中恰好没有第
人,求所抽取的人中恰好没有第![]() 组人的概率.
组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
④“平面向量![]() 与
与![]() 的夹角是钝角”的要条件是“
的夹角是钝角”的要条件是“![]() ”.
”.
其中正确命题的序号是 .(把所有正确命题的序号都写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016 年1 月1 日起全国统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取![]() 后和
后和![]() 后作为调查对象,随机调查了
后作为调查对象,随机调查了![]() 位,得到数据如下表:
位,得到数据如下表:
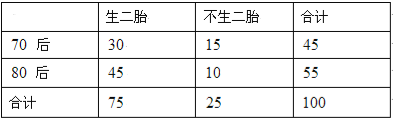
(Ⅰ)以这![]() 个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市
个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市![]() 后公民中随机抽取
后公民中随机抽取![]() 位,记其中生二胎的人数为
位,记其中生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据调查数据,是否有 ![]() 以上的把握认为“生二胎与年龄有关”,并说明理由:
以上的把握认为“生二胎与年龄有关”,并说明理由:
参考数据:

(参考公式: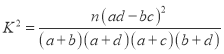 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《选修4—4:坐标系与参数方程》
已知直线l的参数方程为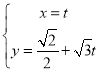 (t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-).
(1)求直线l的倾斜角和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,设点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取4个个体,选取方法从随机数表的第1行第4列数由左到右由上到下开始读取,则选出来的第4个个体的编号为( )
第1行 78 16 65 71 02 30 60 14 01 02 40 60 90 28 01 98
第2行 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.10B.01C.09D.06
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m 、n 与平面α、β给出下列四个命题:
①若m∥l,n∥l,则m∥n; ②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;④若m⊥β,α⊥β,则m∥α
其中,假命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其![]() 下列叙述正确的是( )
下列叙述正确的是( )
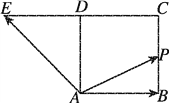
A. 满足λ+μ=2的点P必为BC的中点
B. 满足λ+μ=1的点P有且只有一个
C. λ+μ的最大值为3
D. λ+μ的最小值不存在
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com