
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为坐标原点,点
为坐标原点,点![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() .
.
(1)求椭圆的标准方程;
(2)圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() ,
,![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD= ![]() ,AB=4.
,AB=4. 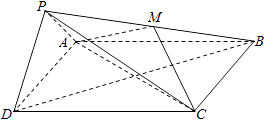
(1)求证:M为PB的中点;
(2)求二面角B﹣PD﹣A的大小;
(3)求直线MC与平面BDP所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,b=2 ![]() ,B=
,B= ![]() .
.
(1)若a=2,求角C;
(2)若D为AC的中点,BD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( ) 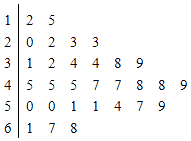
A.46 45 56
B.46 45 53
C.47 45 56
D.45 47 53
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com