【题目】(1)已知椭圆两个焦点的坐标分别是(-2,0)，(2,0)，并且经过点
，求它的标准方程；
（2）已知双曲线两个焦点的坐标分别是(0,-6)，(0,6)，并且经过点(2,-5)，求它的标准方程.
科目：高中数学 来源： 题型：
【题目】某地区高考实行新方案，规定：语文、数学和英语是考生的必考科目，考生还须从物理，化学，生物，历史，地理和政治六个科目中选取三个科目作为选考科目．若一个学生从六个科目中选出了三个科目作为选考科目，则称该学生的选考方案确定；否则，称该学生选考方案待确定．例如，学生甲选择“物理、化学和生物”三个选考科目，则学生甲的选考方案确定，“物理、化学和生物”为其选考方案．
某学校为了解高一年级420名学生选考科目的意向，随机选取30名学生进行了一次调查，统计选考科目人数如下表：
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
（Ⅰ）估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
（Ⅱ）假设男生、女生选择选考科目是相互独立的．从选考方案确定的8位男生中随机选出1人，从选考方案确定的10位女生中随机选出1人，试求该男生和该女生的选考方案中都含有历史学科的概率；
（Ⅲ）从选考方案确定的8名男生中随机选出2名，设随机变量
，求
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四边形
是正方形， 
平面
， 
， 
， 
， 
， 
分别为
， 
， 
的中点.
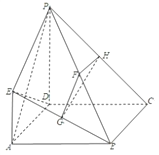
（1）求证： 
平面
；
（2）求平面
与平面
所成锐二面角的大小；
（3）在线段
上是否存在一点
，使直线
与直线
所成的角为
？若存在，求出线段
的长；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出集合
(1)若
求证:函数
(2)由(1)可知，
是周期函数且是奇函数，于是张三同学得出两个命题：
命题甲:集合M中的元素都是周期函数；命题乙:集合M中的元素都是奇函数，请对此给出判断，如果正确，请证明；如果不正确,请举出反例；
(3)设
为常数,且
求
的充要条件并给出证明.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某学校拟建一块五边形区域的“读书角”，三角形区域ABE为书籍摆放区，沿着AB、AE处摆放折线形书架（书架宽度不计），四边形区域为BCDE为阅读区，若∠BAE＝60°，∠BCD＝∠CDE＝120°，DE＝3BC＝3CD＝
m．
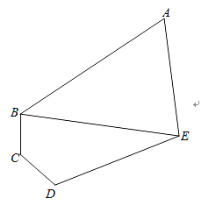
（1）求两区域边界BE的长度；
（2）若区域ABE为锐角三角形，求书架总长度AB+AE的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
零件的个数 |
|
|
|
|
加工的时间 |
|
|
|
|
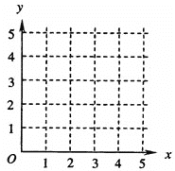
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出
关于
的线性回归方程
.
（3）试预测加工
个零件需要多少时间？
附录：参考公式：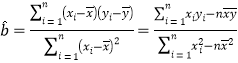
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是2017年第一季度中国某五省
情况图，则下列陈述正确的是（ ）
①2017年第一季度 
总量高于4000亿元的省份共有3个；
②与去年同期相比，2017年第一季度五个省的
总量均实现了增长；
③去年同期的
总量前三位依次是
省、
省、
省；
④2016年同期
省的
总量居于第四位．
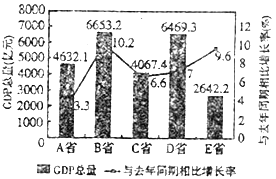
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目：高中数学 来源： 题型：
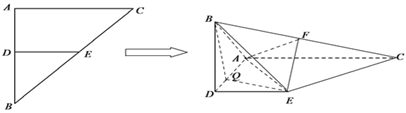
【题目】在等腰
中， 
，腰长为
， 
、
分别是边
、
的中点，将
沿
翻折，得到四棱锥
，且
为棱
中点， 
．
（Ⅰ）求证： 
平面
；
（Ⅱ）在线段
上是否存在一点
，使得
平面
？若存在，求二面角
的余弦值，若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
