
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
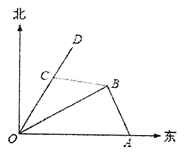
【题目】如图,港口![]() 在港口
在港口![]() 的正东120海里处,小岛
的正东120海里处,小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 的方向,且在港口
的方向,且在港口![]() 北偏西
北偏西![]() 的方向上,一艘科学考察船从港口
的方向上,一艘科学考察船从港口![]() 出发,沿北偏东
出发,沿北偏东![]() 的
的![]() 方向以20海里/小时的速度驶离港口
方向以20海里/小时的速度驶离港口![]() .一艘给养快艇从港口
.一艘给养快艇从港口![]() 以60海里/小时的速度驶向小岛
以60海里/小时的速度驶向小岛![]() ,在
,在![]() 岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
(1)求给养快艇从港口![]() 到小岛
到小岛![]() 的航行时间;
的航行时间;
(2)给养快艇驶离港口![]() 后,最少经过多少小时能和科考船相遇?
后,最少经过多少小时能和科考船相遇?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】恩格尔系数(记为![]() )是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
)是指居民的食物支出占家庭消费总支出的比重.国际上常用恩格尔系数来衡量一个国家和地区人民生活水平的状况.联合国对消费水平的规定标准如下表:
家庭类型 | 贫穷 | 温饱 | 小康 | 富裕 | 最富裕 |
|
|
|
|
|
|
实施精准扶贫以来,根据对某山区贫困家庭消费支出情况(单位:万元)的抽样调查,2018年每个家庭平均消费支出总额为2万元,其中食物消费支出为1.2万元预测2018年到2020年每个家庭平均消费支出总额每年的增长率约是30%,而食物消费支出平均每年增加0.2万元,预测该山区的家庭2020年将处于( )
A.贫困水平B.温饱水平C.小康水平D.富裕水平
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
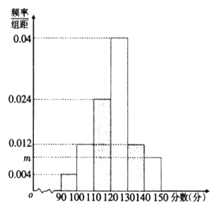
(1)求![]() 的值;并且计算这50名同学数学成绩的样本平均数
的值;并且计算这50名同学数学成绩的样本平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,记成绩在
的同学中选出3位作为代表进行座谈,记成绩在![]() 的同学人数位
的同学人数位![]() ,写出
,写出![]() 的分布列,并求出期望.
的分布列,并求出期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奧斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,他证明过这样一个命题:平面内与两定点距离的比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,设A(﹣3,0),B(3,0),动点M满足![]() =2,则动点M的轨迹方程为()
=2,则动点M的轨迹方程为()
A. (x﹣5)2+y2=16B. x2+(y﹣5)2=9
C. (x+5)2+y2=16D. x2+(y+5)2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,F1、F2为双曲线C:![]() 的左、右焦点,动点P(x0,y0)(y0≥1)在双曲线C的右支上.设∠F1PF2的平分线与x轴、y轴分别交于点M(m,0)、N.
的左、右焦点,动点P(x0,y0)(y0≥1)在双曲线C的右支上.设∠F1PF2的平分线与x轴、y轴分别交于点M(m,0)、N.

(1)求m的取值范围;
(2)设过点F1、N的直线l与双曲线C交于D、E两点,求△F2DE面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设曲线![]() 在原点处切线与直线
在原点处切线与直线![]() 垂直,则a=______.
垂直,则a=______.
(2)已知等差数列![]() 中,已知
中,已知![]() ,则
,则![]() =________________.
=________________.
(3)若函数![]() ,则
,则![]() __________.
__________.
(4)曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的图形的面积为__________.
轴围成的图形的面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() ,
, ![]() :
: ![]() ,和两点
,和两点![]() (0,1),
(0,1),![]() (-1,0),给出如下结论:
(-1,0),给出如下结论:
①不论![]() 为何值时,
为何值时, ![]() 与
与![]() 都互相垂直;
都互相垂直;
②当![]() 变化时,
变化时, ![]() 与
与![]() 分别经过定点A(0,1)和B(-1,0);
分别经过定点A(0,1)和B(-1,0);
③不论![]() 为何值时,
为何值时, ![]() 与
与![]() 都关于直线
都关于直线![]() 对称;
对称;
④如果![]() 与
与![]() 交于点
交于点![]() ,则
,则![]() 的最大值是1;
的最大值是1;
其中,所有正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com