
【题目】已知函数![]()
![]() 常数
常数![]() )满足
)满足![]() .
.
(1)求出![]() 的值,并就常数
的值,并就常数![]() 的不同取值讨论函数
的不同取值讨论函数![]() 奇偶性;
奇偶性;
(2)若![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,当![]() 取最小值时,证明:
取最小值时,证明:![]() 恰有一个零点
恰有一个零点![]() 且存在递增的正整数数列
且存在递增的正整数数列![]() ,使得
,使得![]() 成立.
成立.
【答案】(1)![]() ,
,![]() 时是偶函数,
时是偶函数,![]() 时,非奇非偶函数;(2)
时,非奇非偶函数;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题(1)直接代入已知![]() 可求得
可求得![]() ,根据奇偶函数的定义可说明函数是奇(偶)函数,如果要说明它不是奇(偶)函数,可举例说明,即
,根据奇偶函数的定义可说明函数是奇(偶)函数,如果要说明它不是奇(偶)函数,可举例说明,即![]() 或
或![]() ;(2)据题意,即当
;(2)据题意,即当![]() 时,总有
时,总有![]() 成立,变形整理可得
成立,变形整理可得![]() ,由于分母
,由于分母![]() ,故
,故![]() ,即
,即![]() ,注意到
,注意到![]() ,
,![]() ,从而
,从而![]() ,因此有
,因此有![]() ;(3)在(2)的条件下,
;(3)在(2)的条件下,![]() ,理论上讲应用求出零点
,理论上讲应用求出零点![]() ,由函数表达式可看出,当
,由函数表达式可看出,当![]() 时,无零点,当
时,无零点,当![]() 时,函数
时,函数![]() 是递增函数,如有零点,只有一个,解方程
是递增函数,如有零点,只有一个,解方程![]() ,即
,即![]() ,根据零点存在定理确定出
,根据零点存在定理确定出![]() ,这个三次方程具体的解求不出,但可变形为
,这个三次方程具体的解求不出,但可变形为![]() ,想到无穷递缩等比数列的和,有
,想到无穷递缩等比数列的和,有![]() ,因此可取
,因此可取![]() .证毕.
.证毕.
(1)由![]() 得
得![]() ,解得
,解得![]() .
.
从而![]() ,定义域为
,定义域为![]()
当![]() 时,对于定义域内的任意
时,对于定义域内的任意![]() ,有
,有![]() ,
,![]() 为偶函数 2分
为偶函数 2分
当![]() 时,
时,![]() 从而
从而![]() ,
,![]() 不是奇函数;
不是奇函数;![]() ,
,![]() 不是偶函数,
不是偶函数,![]() 非奇非偶. 4分
非奇非偶. 4分
(2)对于任意的![]() ,总有
,总有![]() 恒成立,即
恒成立,即![]() ,得
,得![]() . 6分
. 6分
![]()
![]() ,
,![]() ,
,![]() ,从而
,从而![]() .
.
又![]() ,∴
,∴![]() ,
,![]() 的最小值等于
的最小值等于![]() . 10分
. 10分
(3)在(2)的条件下,![]() .
.
当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 无零点. 12分
无零点. 12分
当![]() 时,对于任意的
时,对于任意的![]() ,恒有
,恒有![]() ,
,
即![]() ,所以函数
,所以函数![]() 在
在![]() 上递增,又
上递增,又![]() ,
,![]() ,
,
![]()
![]() 在
在![]() 是有一个零点
是有一个零点![]() .
.
综上![]() 恰有一个零点
恰有一个零点![]() ,且
,且![]() 15分
15分
![]() ,得
,得![]() ,
,
又![]() ,故
,故![]() ,
,
取![]() 18分
18分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1(-
(a>b>0)的两个焦点分别为F1(-![]() ,0)、F2(
,0)、F2(![]() ,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)已知点N的坐标为(3,2),点P的坐标为(m,n)(m≠3).过点M任作直线l与椭圆C相交于A、B两点,设直线AN、NP、BN的斜率分别为k1、k2、k3,若k1+k3=2k2,试求m,n满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在第二届乌镇互联网大会中,为了提高安保的级别同时又为了方便接待,现将其中的五个参会国的人员安排酒店住宿,这五个参会国要在![]() 、
、![]() 、
、![]() 三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有_________(填具体数字)
三家酒店选择一家,且每家酒店至少有一个参会国入住,则这样的安排方法共有_________(填具体数字)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为
,上顶点为![]() ,在
,在![]() 轴负半轴上有一点
轴负半轴上有一点![]() ,满足
,满足![]() 为线段
为线段![]() 的中点,且
的中点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若过![]() 、
、![]() 、
、![]() 三点的圆与直线
三点的圆与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(3)在(2)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得以
使得以![]() 、
、![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种新产品,从产品中抽取100件作为样本,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图.
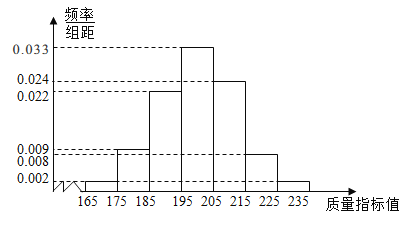
(1)用每组区间的中点值代表该组数据,估算这批产品的样本平均数![]() 和样本方差的
和样本方差的![]() ;
;
(2)从指标值落在![]() 的产品中随机抽取2件做进一步检测,设抽取的产品的指标在
的产品中随机抽取2件做进一步检测,设抽取的产品的指标在![]() 的件数为
的件数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由频率分布直方图可以认为,这种产品的质量指标值服从正态分布![]() ,
,![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,若产品质量指标值大于236.6,则产品不合格,该厂生产10万件该产品,求这批产品不合格的件数.
,若产品质量指标值大于236.6,则产品不合格,该厂生产10万件该产品,求这批产品不合格的件数.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
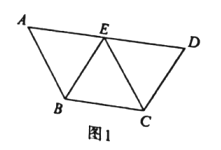
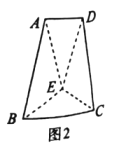
(1)若在平面BCE内存在点G,使得GD∥平面ABE,请问点G的轨迹是什么图形?并说明理由.
(2)求平面AED与平面BCE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着![]() 网络的普及和智能手机的更新换代,各种方便的
网络的普及和智能手机的更新换代,各种方便的![]() 相继出世,其功能也是五花八门.某大学为了调查在校大学生使用
相继出世,其功能也是五花八门.某大学为了调查在校大学生使用![]() 的主要用途,随机抽取了
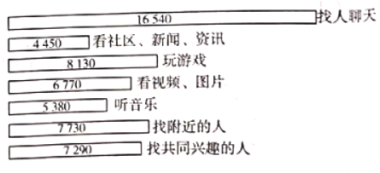
的主要用途,随机抽取了![]() 名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
名大学生进行调查,各主要用途与对应人数的结果统计如图所示,现有如下说法:
①可以估计使用![]() 主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
主要听音乐的大学生人数多于主要看社区、新闻、资讯的大学生人数;
②可以估计不足![]() 的大学生使用
的大学生使用![]() 主要玩游戏;
主要玩游戏;
③可以估计使用![]() 主要找人聊天的大学生超过总数的
主要找人聊天的大学生超过总数的![]() .
.
其中正确的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com