Question

【题目】已知函数f（x）= ，若不等式f（﹣2m2+2m﹣1）+f（8m+ek）＞0（e是自然对数的底数），对任意的m∈[﹣2，4]恒成立，则整数k的最小值是（ ）
A.2
B.3
C.4
D.5

Answer 1

【答案】C
【解析】解：∵f（﹣x）= = =﹣ =﹣f（x）， ∴函数f（x）是奇函数，
函数f（x）= ．定义域为R，函数f（x）在R上是增函数．
证明：设x1 ， x2是R内任意两个值，且x1＜x2 ．
则 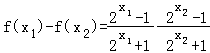= 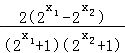①．
又因为x1＜x2 ， 所以 ，又 ．
所以①＜0，即f（x1）﹣f（x2）＜0，即f（x1）＜f（x2）．
故f（x）是R上的增函数．
则不等式若不等式f（﹣2m2+2m﹣1）+f（8m+ek）＞0等价为若不等式f（8m+ek）＞﹣f（﹣2m2+2m﹣1）=f（2m2﹣2m+1），
即8m+ek＞2m2﹣2m+1，
即ek＞2m2﹣10m+1，
设g（m）=2m2﹣10m+1，则函数的对称轴为m= = ，
则当m∈[﹣2，4]时，当m=﹣2时，函数g（m）取得最大值g（﹣2）=29，
即ek＞g（m）max=29，
则k＞ln29．
∵k是整数，
∴k的最小值是4，
故选：C．