
从某校高二年级 名男生中随机抽取
名男生中随机抽取 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组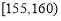 ,第二组
,第二组 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
分组 | 频数 | 频率 | 频率/组距 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
频率分布直方图如下:

(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: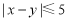 的事件的概率.
的事件的概率.
(1)详见解析;(2)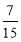 .
.
【解析】
试题分析:(1)由频率和为1,及题设条件得出样本中6、7组的人数为7人,由已知:x+m=7,x,m,2成等差数列,故可求得答案.
(2) 从身高属于第6组和第8组的所有男生中随机的抽取2名男生,记他们的身高分别为x、y,求满足:|x-y|≤5事件的概率,这是一个古典概率模型的问题.用列举法列出基本事件的个数与事件工包含的基本事件数,用古典概率模型的公式求概率..
试题解析:(1) 由频率分布直方图得前五组的频率是
 ,
,
第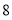 组的频率是
组的频率是 ,所以第
,所以第 组的频率是
组的频率是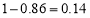 ,所以样本中第
,所以样本中第 组的总人数为
组的总人数为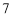 人.由已知得:
人.由已知得:  ①
①
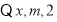 成等差数列,
成等差数列, ②
②
由①②得: ,所以
,所以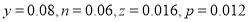 4分
4分
频率分布直方图如下图所示:
 6分
6分
(2)由(1)知,身高在 内的有
内的有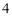 人,设为
人,设为 ,身高在
,身高在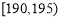 内的有
内的有 人,设为
人,设为
若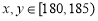 ,则有
,则有 共
共 种情况;
种情况;
若 ,则有
,则有 共
共 种情况;
种情况;
若 ,
, 或
或 ,
, ,则有
,则有
 共
共 种情况
种情况
∴基本事件总数为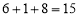 ,而事件 “
,而事件 “ ”所包含的基本事件数为
”所包含的基本事件数为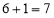 ,故
,故 . 14分
. 14分
考点:1.频率分布直方图;2.等可能事件的概率..


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:2015届湖南张家界市高二上学期期末联考文科数学试卷(解析版) 题型:选择题
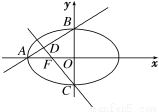
如图所示,椭圆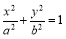 (
(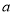 >b>0)的离心率e=
>b>0)的离心率e=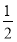 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠BDC的值等于 ( )
A.3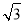 B.
B.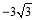
C.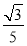 D.
D.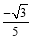
查看答案和解析>>
科目:高中数学 来源:2015届湖北部分重点中学高二上学期期末考试文科数学试卷(解析版) 题型:选择题
右图1是一个水平摆放的小正方体木块,
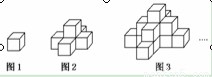
图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是( )
A.25 B.66 C.91 D.120
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测理数学试卷(解析版) 题型:填空题
某中学高一年级有学生600人,高二年级有学生450人,高三年级有学生750人,每个学生被抽到的可能性均为0.2,若该校取一个容量为n的样本,则n= .
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测文数学试卷(解析版) 题型:填空题
欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.已知铜钱是直径为4cm的圆面,中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴不出边界),则油滴整体(油滴是直径为0.2cm的球)正好落入孔中的概率是 (不作近似计算) .
查看答案和解析>>
科目:高中数学 来源:2015届湖北荆门市高二上学期期末质量检测文数学试卷(解析版) 题型:选择题
给定两个命题p,q,若﹁p是q的必要而不充分条件,则p是﹁q的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届湖北孝感高级中学高二上学期期末考试理科数学试卷(解析版) 题型:填空题
设函数f(x)= x3+
x3+ x2,其中θ∈
x2,其中θ∈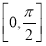 ,则导数f ′(1)的取值范围是_______.
,则导数f ′(1)的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源:2015届浙江省台州市高二第一学期期末数学试卷(解析版) 题型:填空题
已知三棱锥 ,侧棱
,侧棱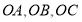 两两互相垂直,且
两两互相垂直,且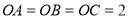 ,则以
,则以 为球心且1为半径的球与三棱锥
为球心且1为半径的球与三棱锥 重叠部分的体积是 .
重叠部分的体积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com