
����Ŀ��2018�꣬�ڡ�������˵�ҡ����ļ����Ŀ�У�Ӣ��������ѧ��ѧ����˹��ġ���ѧ֮�������ݽ���Ƶ��������Ȧ���ϱ�ת���������ӽǶ��أ�������Ĭ����������������̵�ӡ��ij����Ϊ���˽���ڶԸ��ݽ���ϲ���̶ȣ���������˹ۿ��˸��ݽ���140�����ڣ��õ����µ�������������λ������
�� | Ů | �ܼ� | |
ϲ�� | 40 | 60 | 100 |
��ϲ�� | 20 | 20 | 40 |
�ܼ� | 60 | 80 | 140 |
��1���������������������ܷ��ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����Ա���ϲ�����ݽ��йأ�����ȷ��0��001��
��2������60���й����а��Ը��ݽ��Ƿ�ϲ����ȡ�ֲ��������ȡһ������Ϊ6��������Ȼ�����ѡȡ���������ٵ��飬��ѡ�����������ڶ�ϲ�����ݽ��ĸ��ʣ�
�����ٽ�ֵ��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
�ο���ʽ��![]() ��
��![]() ��
��
���𰸡���1������������2��0.4
��������
(1)���ݶ����Լ������![]() �����ò����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����Ա���ϲ�����ݽ��йأ���2�����ùŵ������ѡ�����������ڶ�ϲ�����ݽ��ĸ��ʣ�
�����ò����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����Ա���ϲ�����ݽ��йأ���2�����ùŵ������ѡ�����������ڶ�ϲ�����ݽ��ĸ��ʣ�
��1�����裺�����Ա���ϲ�����ݽ��أ�����֪���ݿ���ã�
![]()
�� �����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ�����Ա���ϲ�����ݽ��йأ�
��2��������Ϊ![]() ��������ϲ���Ĺ�����40��
��������ϲ���Ĺ�����40��![]() =4����
=4����
��ϲ���Ĺ�����6��4=2����
��ϲ�����ݽ���4�����Թ���Ϊa��b��c��d����ϲ�����ݽ���2�����Թ���Ϊ1��2���� �����¼��ֱ�Ϊ����a��b������a��c������a��d������a��1������a��2������b��c������b��d������b��1������b��2������c��d������c��1������c��2������d��1������d��2������1��2����
����ѡ�����������ڶ�ϲ�����ݽ����¼���6����
�������ΪP��A��=![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±��ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���![]() (��)����Ӧ�������ܺ�
(��)����Ӧ�������ܺ�![]() (��)��ú�ļ����������
(��)��ú�ļ����������
|
|
|
|
|
|
|
|
|
|
(1)������ϱ��ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
(2)��֪�ó�����ǰ100�ּײ�Ʒ�������ܺ�Ϊ90�ֱ�ú���Ը���(1)��������Իع鷽�̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ���Ͷ��ٶֱ�ú?
�ο���ʽ��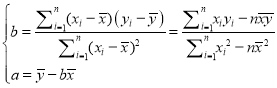
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f(x)��sin 2x��![]() cos 2xͼ�������е�ĺ������쳤��ԭ����2��(�����겻��)���ٽ�ͼ�������е�����ƽ��
cos 2xͼ�������е�ĺ������쳤��ԭ����2��(�����겻��)���ٽ�ͼ�������е�����ƽ��![]() ����λ���ȣ��õ�����g(x)��ͼ����g(x)ͼ���һ���Գ��᷽����(����)
����λ���ȣ��õ�����g(x)��ͼ����g(x)ͼ���һ���Գ��᷽����(����)
A. x����![]() B. x��
B. x��![]()
C. x��![]() D. x��
D. x��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC-A1B1C1�У�AB=3��AA1=4��MΪAA1���е㣬P��BC�ϵ�һ�㣬����P���������澭����CC1��M�����·�߳�Ϊ![]() �����������·����CC1�Ľ���ΪN����
�����������·����CC1�Ľ���ΪN����

��1�����������IJ���չ��ͼ�ĶԽ��ߵij���
��2��PC��NC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ֱ������ϵ�У�����![]() ��
�� ![]() ���������任
���������任![]() ��õ�����
��õ�����![]() .������ԭ��
.������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
�����������![]() ��
��![]() �IJ������̣�
�IJ������̣�
������![]() ��
��![]() �ֱ�������
�ֱ�������![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() (
(![]() ����Ȼ�����ĵ���)��
����Ȼ�����ĵ���)�� ![]() .
.
��1��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
��2����![]() �ĵ������䣻
�ĵ������䣻
��3����![]() ������
������![]() Ϊ
Ϊ![]() �ĵ�������֤����������
�ĵ�������֤����������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��F�ֱ���BC��CD���е㣬G��EF���е㣬������AE��AF��EF������������۳�һ���ռ�ͼ�Σ�ʹB��C��D�����غϣ��غϺ�ĵ��ΪH����ô��������ռ�ͼ���б��У�������
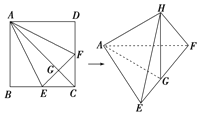
A. ![]() ����ƽ��B.
����ƽ��B. ![]() ����ƽ��
����ƽ��
C. ![]() ����ƽ��D.
����ƽ��D. ![]() ����ƽ��
����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������˶�Ա����Ӱ��ؽ����Ĵ����ѵ������������������ͳ�ƣ�������Ƴɼ���������8�����ɼ������������ƣ����Ҽ�������ɼ����������ķֲ������£�
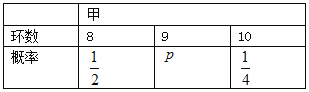
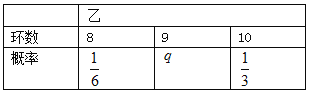
��I����![]() ��
�� ![]() ��ֵ��
��ֵ��
��II�������������ָ�������Σ����Ĵ������ǡ����������9���ĸ��ʣ�
��III�����������ָ����1�Σ����������û����IJ�ľ���ֵΪ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com