
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否存在?若存在,求直线
是否存在?若存在,求直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 存在,且直线
存在,且直线![]() 的斜率
的斜率![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)由题意,![]() ,
,![]() 解方程组即可;
解方程组即可;
(2)分直线![]() 垂直于
垂直于![]() 轴和直线
轴和直线![]() 不垂直于
不垂直于![]() 轴两种情况讨论,当直线
轴两种情况讨论,当直线![]() 垂直于
垂直于![]() 轴时,易得
轴时,易得![]() ,
,![]() ,
,![]() ,不符合题意;当直线
,不符合题意;当直线![]() 不垂直于
不垂直于![]() 轴时,设
轴时,设![]() ,
,![]() ,直线
,直线![]() 方程为
方程为![]() ,联立椭圆方程得到根与系数的关系,代入
,联立椭圆方程得到根与系数的关系,代入![]() 的坐标表示中,即可得到关于
的坐标表示中,即可得到关于![]() 的不等式,解不等式即可.
的不等式,解不等式即可.
(1)设椭圆![]() 的半焦距为
的半焦距为![]() .
.
在![]() 中,令
中,令![]() ,得
,得![]() ,解得
,解得![]() .
.
由垂径长(即过焦点且垂直于实轴的直线与椭圆![]() 相交所得的弦长)为3,
相交所得的弦长)为3,
得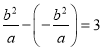 ,
,
所以![]() .①
.①
因为直线![]() 与椭圆
与椭圆![]() 相切,则
相切,则![]() .②
.②
将②代入①,得![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设点![]() ,
,![]() .
.
易知点![]() ,当直线
,当直线![]() 的斜率存在时,设为
的斜率存在时,设为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立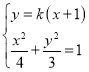 ,得
,得![]() ,
,
则![]() 恒成立.
恒成立.
所以![]() ,
,![]() ,
,
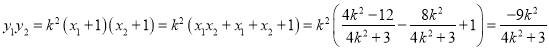 .
.
因为![]() ,
,
所以![]() ,即
,即![]() .
.
即![]() ,
,
得![]() ,得
,得![]() ,
,
即![]() ,解得
,解得![]() .
.
当直线![]() 的斜率
的斜率![]() 不存在时,点
不存在时,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,
此时,![]() ,不符合题意,故舍去.
,不符合题意,故舍去.
综上,直线![]() 存在,且直线
存在,且直线![]() 的斜率
的斜率![]() 的取值范围是
的取值范围是![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣sinx(a∈R).
(1)当![]() 时,f(x)
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=1.
(α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=1.
(1)求C1的极坐标方程,并求C1与C2交点的极坐标![]() ;
;
(2)若曲线C3:θ=β(ρ>0)与C1,C2的交点分别为M,N,求|OM||ON|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,A、B、C、D四地新增疑似病例数据信息如下:
A地:中位数为2,极差为5; B地:总体平均数为2,众数为2;
C地:总体平均数为1,总体方差大于0; D地:总体平均数为2,总体方差为3.
则以上四地中,一定符合没有发生大规模群体感染标志的是_______(填A、B、C、D)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,港口A在港口O的正东100海里处,在北偏东方向有条直线航道OD,航道和正东方向之间有一片以B为圆心,半径为![]() 海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB=
海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB=![]() 海里,tan∠AOB=
海里,tan∠AOB=![]() ,cos∠AOD=
,cos∠AOD=![]() ,现一艘科考船以
,现一艘科考船以![]() 海里/小时的速度从O出发沿OD方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A出发,并沿直线方向行驶与科考船恰好相遇.
海里/小时的速度从O出发沿OD方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A出发,并沿直线方向行驶与科考船恰好相遇.
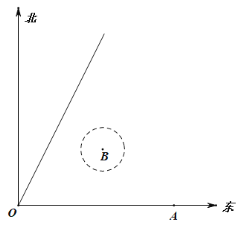
(1)若快艇立即出发,判断快艇是否有触礁的危险,并说明理由;
(2)在无触礁危险的情况下,若快艇再等x小时出发,求x的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过椭圆
过椭圆![]() 的左、右焦点
的左、右焦点![]() 和短轴的端点
和短轴的端点![]() (点
(点![]() 在点
在点![]() 上方).
上方).![]() 为圆
为圆![]() 上的动点(点
上的动点(点![]() 不与
不与![]() 重合),直线
重合),直线![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,其中点
,其中点![]() 构成四边形.
构成四边形.
(1)求椭圆的标准方程;
(2)求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为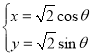 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为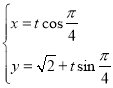 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若点![]() 的极坐标为
的极坐标为![]() ,设曲线
,设曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,则在曲线
,则在曲线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的直角坐标,若不存在,请说明理由.
的直角坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com