
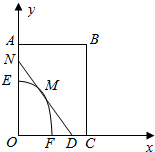
 如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.
如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.分析 (1)求当$t=\frac{2}{3}$ 时,代入函数y=-x2+2,得M($\frac{2}{3}$,$\frac{14}{9}$),利用求函数的导函数得到切线的斜率,运用点斜式写切线方程;
(Ⅱ)求出x=t时的抛物线的切线方程,进一步求出切线截正方形在直线右上方的长度,利用三角形面积公式写出面积,得到的面积是关于t的函数,利用导数分析面积函数在(0<t<2)上的极值,进而得出地块OABC在直路l不含泳池那侧的面积取到最大值.
解答 解:(1)把$t=\frac{2}{3}$代入函数y=-x2+2,得M($\frac{2}{3}$,$\frac{14}{9}$),
∵y'=-2x,
∴k=-$\frac{4}{3}$,
∴直线方程为y=-$\frac{4}{3}$x+$\frac{22}{9}$;
(2)由(1)知,直线的方程为y=-2tx+t2+2,
令y=0,x=$\frac{1}{2}$(t+$\frac{2}{t}$),令x=0,y=t2+2,
∴$\frac{1}{2}$(t+$\frac{2}{t}$)≤2,t2+2≤3,
∴2-$\sqrt{2}$≤t≤1,
∴s△OND=$\frac{1}{2}$$\frac{1}{2}$(t+$\frac{2}{t}$)(t2+2)=$\frac{1}{4}$(t3+4t+$\frac{4}{t}$),
令g(t)=$\frac{1}{4}$(t3+4t+$\frac{4}{t}$),
∴g'(t)=$\frac{({t}^{2}+2)(3{t}^{2}-2)}{4{t}^{2}}$,
当t=$\frac{\sqrt{6}}{3}$时,g'(t)=0,
当t∈(2-$\sqrt{2}$,$\frac{\sqrt{6}}{3}$)时,g'(t)<0,
当t∈($\frac{\sqrt{6}}{3}$,1)时,g'(t)>0,
g(t)≥g($\frac{\sqrt{6}}{3}$)=$\frac{8}{9}\sqrt{6}$,
所以所求面积的最大值为6-$\frac{8}{9}\sqrt{6}$.
点评 利用导数研究函数的单调性;函数模型的选择与应用.


科目:高中数学 来源: 题型:选择题
| A. | (1+x)2=2000 | B. | 2000(1+x)2=3600 | ||
| C. | (3600-2000)(1+x)=3600 | D. | (3600-2000)(1+x)2=3600 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1或-$\frac{1}{2}$ | D. | 1或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | A∈B | C. | A与B无关系 | D. | A?B |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com