Question

【题目】已知函数.

（1）讨论函数的单调性；

（2）定义：“对于在区域上有定义的函数和，若满足恒成立，则称曲线为曲线在区域上的紧邻曲线”.试问曲线与曲线是否存在相同的紧邻直线，若存在，请求出实数的值；若不存在，请说明理由.

Answer 1

【答案】(1) 当时，在上单调递减；当时，在上单调递减，在上单调递增;(2)见解析.

【解析】分析：（1）先求导，再对m分类讨论，求出函数的单调性.(2)先把命题等价转化为曲线与曲线是否相同的外公切线，再去求两支曲线的外公切线令它们相等，最后转化为唯一解问题求出m的值.

详解：（1）.

当时，，函数在上单调递减；

当时，令，得，函数在上单调递减；

令，得，函数在上单调递增.

综上所述，当时，在上单调递减；

当时，在上单调递减，在上单调递增.

（2）原命题等价于曲线与曲线是否相同的外公切线.

函数在点处的切线方程为

，即，

曲线在点处的切线方程为，即.

曲线与的图象有且仅有一条外公切线，

所以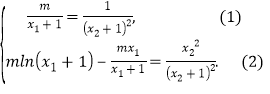

有唯一一对满足这个方程组，且，

由（1）得代入（2）消去，整理得，

关于的方程有唯一解.

令，

∴.

当时，在上单调递减，在上单调递增；

所以.

因为，；，，只需.

令，在为单减函数，

且时，，即，

所以时，关于的方程有唯一解，

此时，外公切线的方程为.

∴这两条曲线存在相同的紧邻直线，此时.