
(1)log0.27和log0.29;
(2)log35和log65;
(3)(lgm)1.9和(lgm)2.1(m>1);
(4)log85和lg4.
思路解析:本题大小比较代表了几个典型的题型.其中题(1)是直接利用对数函数的单调性;题(2)是对数函数底数变化规律的应用;题(3)是指数函数单调性及对数函数性质的综合运用;题(4)是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的增减性.常用的中间量有0、1、2等可通过估算加以选择.
(1)log0.27和log0.29可看作是函数y=log0.2x当x=7和x=9时对应的两函数值,由y=log0.2x在(0,+∞)上单调递减,得log0.27>log0.29.
(2)考察函数y= loga x底数a>1的底数变化规律,函数y=log3x(x>1)的图象在函数y=log6x(x>1)的上方,故log35>log65.
(3)把lgm看作指数函数的底数,要比较两数的大小,关键是比较底数lgm与1的关系.若lgm>1即m>10,则(lgm)x在R上单调递增,故(lgm)1.9<(lgm)2.1.若0<lgm<1即1<m<10,则(lgm)x在R上单调递减,故(lgm)1.9>(lgm)2.1.若lgm=1即m=10,则(lgm)1.9=(lgm)2.1.
(4)因为底数8、10均大于1,且10>8,所以log85>lg5>lg4,即log85>lg4.
答案:(1)log0.27>log0.29.(2)log35>log65.(3)m>10时,(lgm)1.9<(lgm)2.1;m=10时,lgm=1,(lgm)1.9=(lgm)2.1;1<m<10时,(lgm)1.9>(lgm)2.1.(4)log85>lg4.


科目:高中数学 来源:辽宁省沈阳二中2011-2012学年高二上学期12月月考数学试题 题型:044
抛物线y2=4px(p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),比较x0与3p大小;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,求![]() +
+![]() +…+
+…+![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:山东省临清三中2011-2012学年高二12月月考数学试题 题型:044
抛物线y2=4px(p>0)的准线与x轴交于M点,过点M作直线l交抛物线于A、B两点.
(1)若线段AB的垂直平分线交x轴于N(x0,0),比较x0与3p大小;
(2)若直线l的斜率依次为p,p2,p3,…,线段AB的垂直平分线与x轴的交点依次为N1,N2,N3,…,求![]() +
+![]() +…+
+…+![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
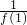 +
+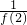 +…+
+…+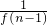 ].
].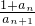 与
与 的大小.
的大小. )(1+
)(1+ )(1+
)(1+ )L(1+
)L(1+ )与4的大小.
)与4的大小.查看答案和解析>>
科目:高中数学 来源:2011年四川省宜宾市南溪一中高考数学一诊模拟试卷1(文科)(解析版) 题型:解答题
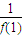 +
+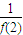 +…+
+…+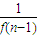 ].
].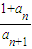 与
与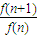 的大小.
的大小.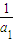 )(1+
)(1+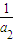 )(1+
)(1+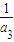 )L(1+
)L(1+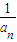 )与4的大小.
)与4的大小.查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题
(1)N个复数一定不能比较大小
(2)z1,z2∈C,若z12+z22==0则z1=z2=0
(3)若实数![]() 与
与![]() 对应,则实数集与纯虚数集一一对应
对应,则实数集与纯虚数集一一对应
(4)若![]() ,
,![]() ∈R,则
∈R,则![]() =
=![]() 是(
是(![]() -
-![]() )+(
)+(![]() +
+![]() )i为纯虚数的充要条件
)i为纯虚数的充要条件
(5)若![]() ,
,![]() ∈R,则
∈R,则![]() +
+![]() i=l+i的充要条件是
i=l+i的充要条件是![]() =
=![]() =1;正确的有( )个
=1;正确的有( )个
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com