
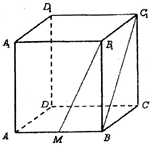
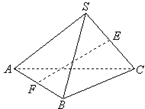
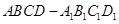 的侧棱长为2,
的侧棱长为2,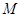 为
为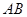 的中点,则异面直线
的中点,则异面直线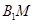 与
与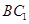 所成角的大小为( )
所成角的大小为( )A.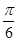 | B.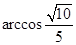 |
C.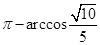 | D.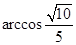 |
科目:高中数学 来源:不详 题型:单选题
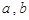 为直线,
为直线, 为平面):
为平面):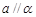 ,
,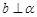 ,则
,则 ;
; ,则过
,则过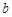 有且只有一个平面与
有且只有一个平面与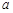 垂直.
垂直.| A.①,② | B.②,③ | C.②,④ | D.③,④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.60º | B.90º | C.45º | D.30º |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,PA=PD=AD=2BC=2,CD
,PA=PD=AD=2BC=2,CD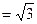 ,M在棱PC上,N是AD的中点,二面角M-BN-C为
,M在棱PC上,N是AD的中点,二面角M-BN-C为 .
.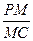 的值;
的值;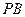 与平面BMN所成角的大小.网
与平面BMN所成角的大小.网
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
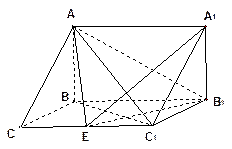
 柱
柱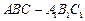 中,已知
中,已知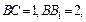
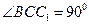 ,
,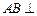 侧面
侧面
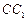 (不包含端点
(不包含端点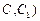 上确定一点
上确定一点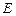 的位置,使得
的位置,使得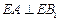 (要求说明理由).
(要求说明理由).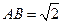 ,求二面角
,求二面角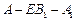 的大小.
的大小.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 角板按图甲方式拼好,其中
角板按图甲方式拼好,其中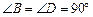 ,
,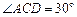 ,
,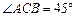 ,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
,AC = 2,现将三角板ACD沿AC折起,使D在平面ABC上的射影O恰好在AB上,如图乙.
 :O为线段AB中点;
:O为线段AB中点;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com