
【题目】某工厂采用甲、乙两种不同生产方式生产某零件,现对两种生产方式所生产的这种零件的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为一等品;指标在区间
的为一等品;指标在区间![]() 的为二等品,现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
的为二等品,现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
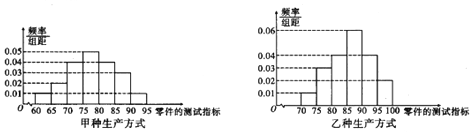
![]() 若从甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取5件,再从这5件零件中随机抽取3件,求至少有1件一等品的概率;
若从甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取5件,再从这5件零件中随机抽取3件,求至少有1件一等品的概率;
![]() 该厂所生产这种零件,若是一等品每件可售50元,若是二等品每件可售20元
该厂所生产这种零件,若是一等品每件可售50元,若是二等品每件可售20元![]() 甲种生产方式每生产一件零件
甲种生产方式每生产一件零件![]() 无论是一等品还是二等品
无论是一等品还是二等品![]() 的成本为10元,乙种生产方式每生产一件零件
的成本为10元,乙种生产方式每生产一件零件![]() 无论是一等品还是二等品
无论是一等品还是二等品![]() 的成本为18元
的成本为18元![]() 将频率分布直方图中的频率视作概率,用样本估计总体比较在甲、乙两种不同生产方式下,哪种生产方式生产的零件所获得的平均利润较高?
将频率分布直方图中的频率视作概率,用样本估计总体比较在甲、乙两种不同生产方式下,哪种生产方式生产的零件所获得的平均利润较高?
【答案】(1)![]() (2) 乙种生产方式
(2) 乙种生产方式
【解析】
(1)先求得100件产品中一等品的数量,按照分层抽样抽取样品,再把所有可能列举出来,即可求得至少有1件一等品的概率。
(2)由频率分布直方图,可得一等品和二等品的概率,根据频率分布直方图可求得两种情况下的平均利润,进而做出选择。
![]() 由甲种生产方式生产的100件零件的测试指标的频率分布直方图可知,
由甲种生产方式生产的100件零件的测试指标的频率分布直方图可知,
这100件样本零件中有一等品:![]() 件
件![]() ,
,
二等品:![]() 件
件![]() ,所以按等级,利用分层抽样的方法抽取的5件零件中有一等品2件,二等品3件.2件一等品用符号
,所以按等级,利用分层抽样的方法抽取的5件零件中有一等品2件,二等品3件.2件一等品用符号![]() ,
,![]() 表示,3件二等品用符号
表示,3件二等品用符号![]() ,
,![]() ,
,![]() 表示,
表示,
则从这5件零件中抽取3件,共有10种可能:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
记事件A为“这5件零件中随机抽取3件,至少有1件一等品”,
事件A包含9个基本事件:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则至少有1件一等品的概率![]()
![]() 由乙种生产方式生产的100件零件的测试指标的频率分布直方图可知,
由乙种生产方式生产的100件零件的测试指标的频率分布直方图可知,
这100件样本零件中,一等品的频率为![]() ,
,
二等品的频率为![]() ,
,
设甲种生产方式每生产一件零件所获得的平均利润为![]() 元,
元,
乙种生产方式每生产一件零件所获得的平均利润为![]() 元,
元,
将频率分布直方图中的频率视作概率,用样本估计总体,
可得![]() 元
元![]() ,
,
![]() 元
元![]() ,
,
由于![]() ,所以乙种生产方式生产的零件所获得的平均利润较高
,所以乙种生产方式生产的零件所获得的平均利润较高![]()


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】在某次投篮测试中,有两种投篮方案:方案甲:先在A点投篮一次,以后都在B点投篮;方案乙:始终在B点投篮.每次投篮之间相互独立.某选手在A点命中的概率为![]() ,命中一次记3分,没有命中得0分;在B点命中的概率为
,命中一次记3分,没有命中得0分;在B点命中的概率为![]() ,命中一次记2分,没有命中得0分,用随机变量
,命中一次记2分,没有命中得0分,用随机变量![]() 表示该选手一次投篮测试的累计得分,如果
表示该选手一次投篮测试的累计得分,如果![]() 的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
(1)若该选手选择方案甲,求测试结束后所得分![]() 的分布列和数学期望.
的分布列和数学期望.
(2)试问该选手选择哪种方案通过测试的可能性较大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD的顶点A,B以及CD的中点P处,已知AB=20km,CB=10km,为了处理三家工厂的污水,现要在矩形ABCD内(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为![]() km.
km.

(I)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(II)确定污水处理厂的位置,使三条排污管道的总长度最短,并求出最短值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下图频率分布直方图:
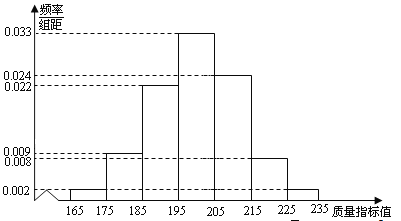
(I)求这500件产品质量指标值的样本平均值![]() 和样本方差
和样本方差![]() (同一组的数据用该组区间的中点值作代表);
(同一组的数据用该组区间的中点值作代表);
(II)由直方图可以认为,这种产品的质量指标![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)某用户从该企业购买了100件这种产品,记![]() 表示这100件产品中质量指标值位于区间
表示这100件产品中质量指标值位于区间![]() 的产品件数.利用(i)的结果,求
的产品件数.利用(i)的结果,求![]() .
.
附:![]()
若![]() 则
则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD,底面ABCD是![]() ,边长为
,边长为![]() 的菱形,又
的菱形,又![]() 底面
底面![]() (即
(即![]() 与底面
与底面![]() 内的任意一条直线垂直),且
内的任意一条直线垂直),且![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点.
的中点.
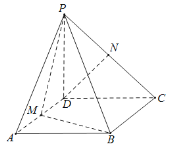
(1)求异面直线![]() 与
与![]() 所成角的余弦值
所成角的余弦值
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知左、右焦点分别为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆C关于直线x=c对称的图形过坐标原点.
,且椭圆C关于直线x=c对称的图形过坐标原点.
(I)求椭圆C的离心率和标准方程。
(II)圆![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线
与椭圆C交于A,B两点,R为线段AB上任一点,直线![]() 交椭圆C于P,Q两点,若AB为圆
交椭圆C于P,Q两点,若AB为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于1,求
的斜率大于1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com