
(本大题12分)定义在R上的单调函数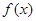 满足
满足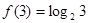 且对任意
且对任意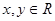 都有
都有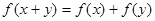 .
.
(1)求证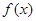 为奇函数;
为奇函数;
(2)若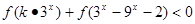 对任意
对任意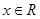 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(1) f(x)是奇函数.证明略
(2) 当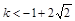 时f(k·3
时f(k·3 )+f(3
)+f(3 -9
-9 -2)<0对任意x∈R恒成立。
-2)<0对任意x∈R恒成立。
【解析】解:(1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.
(2)解:f(3)=log 3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k·3 )<-f(3
)<-f(3 -9
-9 -2)=f(-3
-2)=f(-3 +9
+9 +2), k·3
+2), k·3 <-3
<-3 +9
+9 +2,
+2,
3 -(1+k)·3
-(1+k)·3 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.
令t=3 >0,问题等价于t
>0,问题等价于t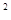 -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.
令 ,其对称轴为
,其对称轴为 ,
,
当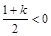 即
即 时,
时,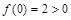 ,符合题意.
,符合题意.
当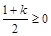 即
即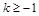 时,对任意
时,对任意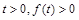 恒成立
恒成立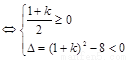
解得: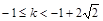
综上,当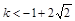 时f(k·3
时f(k·3 )+f(3
)+f(3 -9
-9 -2)<0对任意x∈R恒成立
-2)<0对任意x∈R恒成立


科目:高中数学 来源:2015届福建省四地六高一第三次月考数学试卷(解析版) 题型:解答题
(本小题满分12分)定义在实数R上的函数y= f(x)是偶函数,当x≥0时,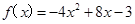 .
.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省偃师市高一第三次月考数学试卷(解析版) 题型:解答题
(本小题满分12分)
定义在 上的偶函数
上的偶函数 ,已知当
,已知当 时的解析式
时的解析式
(Ⅰ)写出 在
在 上的解析式;
上的解析式;
(Ⅱ)求 在
在 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省四地六校高二下学期第一次月考数学理卷 题型:解答题
((本小题12分)某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为
 (单位:万元),成本函数为
(单位:万元),成本函数为 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数 的边际函数
的边际函数 定义为
定义为 。
。
(Ⅰ)求利润函数 及边际利润函数
及边际利润函数 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数 单调递减时
单调递减时 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011年新疆农七七师高级中学高二下学期第一学段考试理科数学 题型:解答题
(本小题12分)
某造船公司年造船量是20艘,已知造船 艘的产值函数为
艘的产值函数为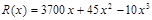 (单位:万元),成本函数为
(单位:万元),成本函数为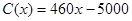 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数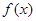 的边际函数
的边际函数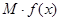 定义为
定义为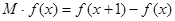 。
。
(Ⅰ)求利润函数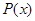 及边际利润函数
及边际利润函数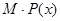 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
(Ⅱ)问年造船量安排多少艘时,可使公司造船的年利润最大?
(Ⅲ)求边际利润函数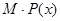 单调递减时
单调递减时 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com