
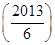 =________.
=________.科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
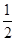 t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 上的零点个数为________.
上的零点个数为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.-3≤x≤2 | B.-2≤x≤3 |
| C.x≤-2或x≥3 | D.x≤-3或x≥2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.f(x)=2x+b,x∈R,x= |
| B.f(x)=ex,x∈R,x=cost |
| C.f(x)=x2,x∈R,x=et |
| D.f(x)=|x|,x∈R,x=lnt |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 x2+10x(万元).当年产量不小于80千件时,C(x)=51x+
x2+10x(万元).当年产量不小于80千件时,C(x)=51x+ -1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com