
【题目】已知![]() 是抛物线
是抛物线![]() 上一点,经过点
上一点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 、
、![]() 分别交直线
分别交直线![]() 于点
于点![]() 、
、![]() .
.
(1)求抛物线方程及其焦点坐标;
(2)求证:以![]() 为直径的圆恰好经过原点.
为直径的圆恰好经过原点.
【答案】(1)抛物线方程为![]() ,焦点坐标为
,焦点坐标为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)将点![]() 的坐标代入抛物线
的坐标代入抛物线![]() 的方程,求出
的方程,求出![]() 的值,可得出抛物线
的值,可得出抛物线![]() 的方程,并求出抛物线
的方程,并求出抛物线![]() 的焦点坐标;
的焦点坐标;
(2)设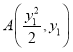 ,
,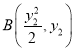 ,
,![]() 、
、![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,其中
,其中![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,列出韦达定理,利用向量共线求出点
的方程联立,列出韦达定理,利用向量共线求出点![]() 、
、![]() 的坐标,然后将韦达定理代入
的坐标,然后将韦达定理代入![]() ,利用向量数量积的坐标运算计算出
,利用向量数量积的坐标运算计算出![]() ,即可证明出结论成立.
,即可证明出结论成立.
(1)将![]() 代入
代入![]() ,得
,得![]() ,因此,抛物线方程为
,因此,抛物线方程为![]() ,焦点坐标为
,焦点坐标为![]() ;
;
(2)设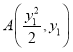 ,
,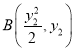 ,
,![]() 、
、![]() .
.
因为直线![]() 不经过点
不经过点![]() ,所以直线
,所以直线![]() 一定有斜率,设直线
一定有斜率,设直线![]() 方程为
方程为![]() ,
,
与抛物线方程联立得到![]() ,消去
,消去![]() ,得
,得![]() ,
,
则由韦达定理得![]() ,
,![]() .
.
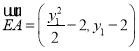 ,
,![]() ,
,
![]() ,
,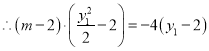 ,即
,即![]() ,
,
显然,![]() ,
,![]() ,
,![]() ,
,
则点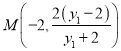 ,同理可求得点
,同理可求得点![]() 的坐标为
的坐标为![]() ,
,
所以,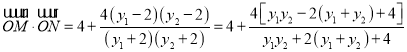
![]() ,
,
![]() ,因此,以
,因此,以![]() 为直径的圆过原点.
为直径的圆过原点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的,下列说法中正确的是( )
A.100个吸烟者中至少有99人患有肺癌
B.1个人吸烟,那么这个人有99%的概率患有肺癌
C.在100个吸烟者中一定有患肺癌的人
D.在100个吸烟者中可能一个患肺癌的人也没有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核.记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了30名学生的考核成绩,并作成如下茎叶图:

(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核优秀的概率;
(Ⅱ)从图中考核成绩满足![]() 的学生中任取3人,设
的学生中任取3人,设![]() 表示这3人中成绩满足
表示这3人中成绩满足![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据以往培训数据,规定当![]() 时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
时培训有效.请根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一辆汽车从![]() 市出发沿海岸一条直公路以
市出发沿海岸一条直公路以![]() 的速度向东匀速行驶,汽车开动时,在
的速度向东匀速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件送给这辆汽车的司机.

(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高三年级学生为了庆祝教师节,同学们为老师制作了一大批同一种规格的手工艺品,这种工艺品有![]()
![]() 两项技术指标需要检测,设各项技术指标达标与否互不影响,若
两项技术指标需要检测,设各项技术指标达标与否互不影响,若![]() 项技术指标达标的概率为
项技术指标达标的概率为![]() 项技术指标达标的概率为
项技术指标达标的概率为![]() ,按质量检验规定:两项技术指标都达标的工艺品为合格品.
,按质量检验规定:两项技术指标都达标的工艺品为合格品.
(1)求一个工艺品经过检测至少一项技术指标达标的概率;
(2)任意依次抽取该工艺品4个,设![]() 表示其中合格品的个数,求
表示其中合格品的个数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,由一块扇形空地![]() ,其中
,其中![]() ,
,![]() 米,计划在此扇形空地区域为学生建灯光篮球运动场,
米,计划在此扇形空地区域为学生建灯光篮球运动场,![]() 区域内安装一批照明灯,点
区域内安装一批照明灯,点![]() 、
、![]() 选在线段
选在线段![]() 上(点
上(点![]() 、
、![]() 分别不与点
分别不与点![]() 、
、![]() 重合),且
重合),且![]() .
.

(1)若![]() 点在距离
点在距离![]() 点
点![]() 米处,求点
米处,求点![]() 、
、![]() 之间的距离;
之间的距离;
(2)为了使运动场地区域最大化,要求![]() 面积尽可能的小,记
面积尽可能的小,记![]() ,请用
,请用![]() 表示
表示![]() 的面积
的面积![]() ,并求
,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com