
ЎѕМвДїЎїBMIЦёКэКЗУГМеЦШ№«ЅпКэіэТФЙнёЯГЧКэµДЖЅ·ЅµГіцµДКэЦµЈ¬КЗ№ъјКЙПіЈУГµДєвБїИЛМеЕЦКЭіМ¶ИТФј°КЗ·сЅЎїµµДТ»ёц±кЧј.¶ФУЪёЯЦРДРМеУэМШі¤Йъ¶шСФЈ¬µ±BMIКэЦµґуУЪ»тµИУЪ20.5К±Ј¬ОТГЗЛµМеЦШЅПЦШЈ¬µ±BMIКэЦµРЎУЪ20.5К±Ј¬ОТГЗЛµМеЦШЅПЗбЈ¬ЙнёЯґуУЪ»тµИУЪ170cmК±Ј¬ОТГЗЛµЙнёЯЅПёЯЈ¬ЙнёЯРЎУЪ170cmК±Ј¬ОТГЗЛµЙнёЯЅП°«.ДіЦРРЎС§ЙъіЙі¤Ул·ўХ№»ъ№№ґУДіКРµД320ГыёЯЦРДРМеУэМШі¤ЙъЦРЛж»ъСЎИЎ8ГыЈ¬ЖдЙнёЯєНМеЦШµДКэѕЭИз±нЛщКѕЈє
±аєЕ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ЙнёЯЈЁcmЈ© | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
МеЦШЈЁkgЈ© | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
ЈЁ1Ј©ёщѕЭЧоРЎ¶юіЛ·ЁµДЛјПлУ빫ʽЗуµГПЯРФ»Ш№й·ЅіМ![]() .АыУГТСѕЗуµГµДПЯРФ»Ш№й·ЅіМЈ¬ЗлНкЙЖПВБРІРІо±нЈ¬ІўЗуЅвКН±дБїЈЁЙнёЯЈ©¶ФУЪФ¤±Ё±дБїЈЁМеЦШЈ©±д»ЇµД№±ПЧЦµ
.АыУГТСѕЗуµГµДПЯРФ»Ш№й·ЅіМЈ¬ЗлНкЙЖПВБРІРІо±нЈ¬ІўЗуЅвКН±дБїЈЁЙнёЯЈ©¶ФУЪФ¤±Ё±дБїЈЁМеЦШЈ©±д»ЇµД№±ПЧЦµ![]() ЈЁ±ЈБфБЅО»УРР§КэЧЦЈ©Ј»
ЈЁ±ЈБфБЅО»УРР§КэЧЦЈ©Ј»
±аєЕ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ЙнёЯЈЁcmЈ© | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
МеЦШЈЁkgЈ© | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
ІРІо | 0.1 | 0.3 | 0.9 | ©Ѓ1.5 | ©Ѓ0.5 |
ЈЁ2Ј©НЁ№эІРІо·ЦОцЈ¬¶ФУЪІРІоµДЧоґуЈЁѕш¶ФЦµЈ©µДДЗЧйКэѕЭЈ¬РиТЄИ·ИПФЪСщ±ѕµгµДІЙјЇЦРКЗ·сУРИЛОЄµДґнОу.ТСЦЄНЁ№эЦШРВІЙјЇ·ўПЦЈ¬ёГЧйКэѕЭµДМеЦШУ¦ёГОЄ58ЈЁkgЈ©.ЗлЦШРВёщѕЭЧоРЎ¶юіЛ·ЁµДЛјПлУ빫ʽЈ¬ЗуіцДРМеУэМШі¤ЙъµДЙнёЯУлМеЦШµДПЯРФ»Ш№й·ЅіМ.
ІОїј№«КЅЈє 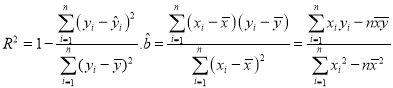 Ј¬
Ј¬![]() .
.![]() .
.
ІОїјКэѕЭЈє![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
Ўѕґр°ёЎїЈЁ1Ј©Мо±нјыЅвОц;![]() ;ЈЁ2Ј©
;ЈЁ2Ј©![]() .
.
ЎѕЅвОцЎї
ЈЁ1Ј©УЙ±нЦРµДКэѕЭїЙЗуіцПЯРФ»Ш№й·ЅіМОЄ![]() Ј¬Ѕш¶шїЙНкЙЖЛщёш±нёсЈ¬ЗуіцЛщУРІРІоЦµ.УЙ
Ј¬Ѕш¶шїЙНкЙЖЛщёш±нёсЈ¬ЗуіцЛщУРІРІоЦµ.УЙ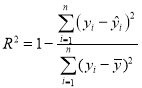 јґїЙЗуіц№±ПЧЦµ
јґїЙЗуіц№±ПЧЦµ![]() .
.
ЈЁ2Ј©јЖЛгРЮ¶©єу![]() ТФј°
ТФј°![]() Ј¬ґъИлµЅ
Ј¬ґъИлµЅ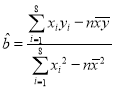 Ј¬
Ј¬![]() Ѕш¶шїЙЗуіцПЯРФ»Ш№й·ЅіМ.
Ѕш¶шїЙЗуіцПЯРФ»Ш№й·ЅіМ.
ЅвЈєЈЁ1Ј©УЙМвТвЦЄПЯРФ»Ш№й·ЅіМОЄ![]() Ј¬јЖЛг
Ј¬јЖЛг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .НкЙЖПВБРІРІо±нИзПВЈ¬
.НкЙЖПВБРІРІо±нИзПВЈ¬
±аєЕ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ЙнёЯЈЁcmЈ©xi | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
МеЦШЈЁkgЈ©yi | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
ІРІо | 0.1 | 0.3 | 0.9 | ©Ѓ1.5 | ©Ѓ0.5 | ©Ѓ2.3 | ©Ѓ0.5 | 3.5 |
јЖЛг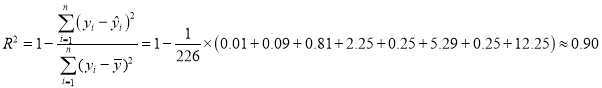 Ј¬
Ј¬
ЛщТФЅвКН±дБїЈЁЙнёЯЈ©¶ФУЪФ¤±Ё±дБїЈЁМеЦШЈ©±д»ЇµД№±ПЧЦµ![]() .
.
ЈЁ2Ј©НЁ№эІРІо·ЦОцЦЄЈ¬ІРІоµДЧоґуЈЁѕш¶ФЦµЈ©µДДЗЧйКэѕЭОЄµЪ8ЧйЈ¬ЗТ![]()
УЙ![]() Ј¬јЖЛгРЮ¶©єу
Ј¬јЖЛгРЮ¶©єу![]()
УЦ![]() Ј¬
Ј¬![]() Ј¬РЮ¶©єу
Ј¬РЮ¶©єу![]() .
.
ЛщТФ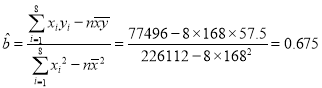 Ј¬
Ј¬
![]() .
.
ЛщТФ![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМКЗ
µДПЯРФ»Ш№й·ЅіМКЗ![]() .
.



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() Ј¬ВъЧг
Ј¬ВъЧг![]() .Йи
.Йи![]() ОЄ
ОЄ![]() ЙПИОТ»µг,№э
ЙПИОТ»µг,№э![]() Чч
Чч![]() µДЗРПЯ,ЖдР±ВК
µДЗРПЯ,ЖдР±ВК![]() ВъЧг
ВъЧг![]()
ЈЁ1Ј©ЗуєЇКэ![]() µДЅвОцКЅЈ»
µДЅвОцКЅЈ»
ЈЁ2Ј©ИфКэБР![]() ВъЧг
ВъЧг![]() .Йи
.Йи![]() ОЄХэіЈКэ.
ОЄХэіЈКэ.
ўЩЗу![]() Ј»
Ј»
ўЪИфІ»µИКЅ![]() ¶ФИОТвµД
¶ФИОТвµД![]() єгіЙБўЈ¬ФтКµКэ
єгіЙБўЈ¬ФтКµКэ![]() КЗ·сґжФЪЧоґуЦµ?ИфґжФЪ,ЗлЗуіцХвёцЦµЈ»ИфІ»ґжФЪ,ЗлЛµГчАнУЙ.
КЗ·сґжФЪЧоґуЦµ?ИфґжФЪ,ЗлЗуіцХвёцЦµЈ»ИфІ»ґжФЪ,ЗлЛµГчАнУЙ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЦ±ПЯ![]() µДІОКэ·ЅіМОЄ
µДІОКэ·ЅіМОЄ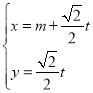 ЈЁ
ЈЁ![]() ОЄІОКэЈ©Ј¬ТФЧш±кФµгОЄј«µгЈ¬
ОЄІОКэЈ©Ј¬ТФЧш±кФµгОЄј«µгЈ¬![]() ЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬ЗъПЯ
ЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬ЗъПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ![]() Ј¬ЗТЗъПЯ
Ј¬ЗТЗъПЯ![]() µДЧуЅ№µг
µДЧуЅ№µг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙП.
ЙП.
ЈЁўсЈ©Зу![]() µДј«Чш±к·ЅіМєНЗъПЯ
µДј«Чш±к·ЅіМєНЗъПЯ![]() µДІОКэ·ЅіМЈ»
µДІОКэ·ЅіМЈ»
ЈЁўтЈ©ЗуЗъПЯ![]() µДДЪЅУѕШРОµДЦЬі¤µДЧоґуЦµ.
µДДЪЅУѕШРОµДЦЬі¤µДЧоґуЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪГчґъіМґуО»ЛщЦшµДЎ¶Лг·ЁНіЧЪЎ·ЦРУРХвСщТ»КЧёиТҐЈ¬Ў°·ЕДБИЛґЦРДґуТвЈ¬ИэРуНµНµіФГзЗаЈ¬ГзЦчїЫЧЎЕЈВнСтЈ¬ТЄЗуЕ⳥Ое¶·БёЈ¬ИэРу»§ЦчФёЕ⳥Ј¬ЕЈВнСтіФµГТмСщЈ®ВніФБЛЕЈµДТ»°лЈ¬СтіФБЛВнµДТ»°лЈ®Ў±ЗлОКёчРуЕв¶аЙЩЈїЛьµДґуТвКЗ·ЕДБИЛ·ЕДБК±ґЦРДґуТвЈ¬ЕЈЎўВнЎўСтНµіФЗаГзЈ¬ЗаГзЦчИЛїЫЧЎЕЈЎўВнЎўСтПтЖдЦчИЛТЄЗуЕ⳥Ое¶·БёКіЈЁ1¶·=10ЙэЈ©Ј¬ИэРуµДЦчИЛН¬ТвЕ⳥Ј¬µ«ЕЈЎўВнЎўСтіФµДЗаГзБїёчІ»ПаН¬Ј®ВніФµДЗаГзКЗЕЈµДТ»°лЈ¬СтіФµДЗаГзКЗВнµДТ»°лЈ®ОКСтЎўВнЎўЕЈµДЦчИЛУ¦ёГ·Ц±рПтЗаГзЦчИЛЕ⳥¶аЙЩЙэБёКіЈїЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїµзУ°Ў¶Ачє¦БЛЈ¬ОТµД№ъЎ·УЪ2018Дк3ФВХэКЅµЗВЅИ«№ъФєПЯЈ¬НшУС·Ч·Ч±нКѕЈ¬їґНкµзУ°ИИСЄ·РМЪЎ°ОТОЄОТµД№ъјТЅѕ°БЈ¬ОТОЄОТКЗЦР№ъИЛЅѕ°БЈЎЎ±Ў¶Ачє¦БЛЈ¬ОТµД№ъЎ·ХэФЪХЩ»ЅОТГЗГїТ»ёцИЛЈ¬І»НьіхРДЈ¬УГ·Ь¶·КйРґОЮ»ЪИЛЙъЈ¬РЎГчПлФјјЧЎўТТЎў±ыЎў¶ЎЛДО»єГЕуУСТ»Н¬ИҐїґЎ¶Ачє¦БЛЈ¬ОТµД№ъЎ·Ј¬Іў°С±кК¶ОЄ![]() µДЛДХЕµзУ°Ж±·ЕФЪ±аєЕ·Ц±рОЄ1Ј¬2Ј¬3Ј¬4µДЛДёцІ»Н¬µДєРЧУАпЈ¬ИГЛДО»єГЕуУСЅшРРІВІвЈє
µДЛДХЕµзУ°Ж±·ЕФЪ±аєЕ·Ц±рОЄ1Ј¬2Ј¬3Ј¬4µДЛДёцІ»Н¬µДєРЧУАпЈ¬ИГЛДО»єГЕуУСЅшРРІВІвЈє
јЧЛµЈєµЪ1ёцєРЧУАп·ЕµДКЗ![]() Ј¬µЪ3ёцєРЧУАп·ЕµДКЗ
Ј¬µЪ3ёцєРЧУАп·ЕµДКЗ![]()
ТТЛµЈєµЪ2ёцєРЧУАп·ЕµДКЗ![]() Ј¬µЪ3ёцєРЧУАп·ЕµДКЗ
Ј¬µЪ3ёцєРЧУАп·ЕµДКЗ![]()
±ыЛµЈєµЪ4ёцєРЧУАп·ЕµДКЗ![]() Ј¬µЪ2ёцєРЧУАп·ЕµДКЗ
Ј¬µЪ2ёцєРЧУАп·ЕµДКЗ![]()
¶ЎЛµЈєµЪ4ёцєРЧУАп·ЕµДКЗ![]() Ј¬µЪ3ёцєРЧУАп·ЕµДКЗ
Ј¬µЪ3ёцєРЧУАп·ЕµДКЗ![]()
РЎГчЛµЈєЎ°ЛДО»ЕуУСДгГЗ¶јЦ»Лµ¶ФБЛТ»°лЎ±
їЙТФФ¤ІвЈ¬µЪ4ёцєРЧУАп·ЕµДµзУ°Ж±ОЄ_________
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэfЈЁxЈ©ЈЅx|x©Ѓa|Ј¬aЎКR.
ЈЁ1Ј©µ±fЈЁ2Ј©+fЈЁ©Ѓ2Ј©Јѕ4К±Ј¬ЗуaµДИЎЦµ·¶О§Ј»
ЈЁ2Ј©ИфaЈѕ0Ј¬xЈ¬yЎКЈЁ©ЃЎЮЈ¬a]Ј¬І»µИКЅfЈЁxЈ©ЎЬ|y+3|+|y©Ѓa|єгіЙБўЈ¬ЗуaµДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЛДАвЧ¶P©ЃABCDЦРADЎОBCЈ¬DAЎНABЈ¬ADЈЅ2Ј¬ABЈЅBCЈЅ1Ј¬CD![]() Ј¬µгEОЄPDЦРµг.
Ј¬µгEОЄPDЦРµг.
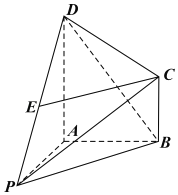
ЈЁ1Ј©ЗуЦ¤ЈєCEЎОЖЅГжPABЈ»
ЈЁ2Ј©ИфPAЈЅ2Ј¬PDЈЅ2![]() Ј¬ЎПPAB
Ј¬ЎПPAB![]() Ј¬ЗуЖЅГжPBDУлЖЅГжECDЛщіЙИс¶юГжЅЗµДУаПТЦµ.
Ј¬ЗуЖЅГжPBDУлЖЅГжECDЛщіЙИс¶юГжЅЗµДУаПТЦµ.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФІМЁ![]() µДЦбЅШГжОЄµИСьМЭРО
µДЦбЅШГжОЄµИСьМЭРО![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ФІМЁ
Ј¬ФІМЁ![]() µДІаГж»эОЄ
µДІаГж»эОЄ![]() .ИфµгCЈ¬D·Ц±рОЄФІ
.ИфµгCЈ¬D·Ц±рОЄФІ![]() Ј¬
Ј¬![]() ЙПµД¶ЇµгЗТµгCЈ¬DФЪЖЅГж
ЙПµД¶ЇµгЗТµгCЈ¬DФЪЖЅГж![]() µДН¬Іа.
µДН¬Іа.
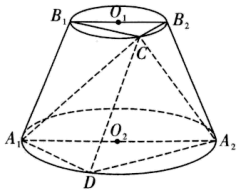
ЈЁ1Ј©ЗуЦ¤Јє![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() Ј¬Фтµ±ИэАвЧ¶
Ј¬Фтµ±ИэАвЧ¶![]() µДМе»эИЎЧоґуЦµК±Ј¬Зу¶аГжМе
µДМе»эИЎЧоґуЦµК±Ј¬Зу¶аГжМе![]() µДМе»э.
µДМе»э.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦР,ТСЦЄЦ±ПЯ
ЦР,ТСЦЄЦ±ПЯ![]() µДІОКэ·ЅіМОЄ
µДІОКэ·ЅіМОЄ ЈЁ
ЈЁ![]() ОЄІОКэЈ©.ФЪТФЧш±кФµг
ОЄІОКэЈ©.ФЪТФЧш±кФµг![]() ОЄј«µг,
ОЄј«µг,![]() ЦбµДХэ°лЦбОЄј«Цб,ЗТУлЦ±ЅЗЧш±кПµі¤¶ИµҐО»ПаН¬µДј«Чш±кПµЦР,ЗъПЯ
ЦбµДХэ°лЦбОЄј«Цб,ЗТУлЦ±ЅЗЧш±кПµі¤¶ИµҐО»ПаН¬µДј«Чш±кПµЦР,ЗъПЯ![]() µДј«Чш±к·ЅіМКЗ
µДј«Чш±к·ЅіМКЗ![]() .
.
ЈЁ1Ј©ЗуЦ±ПЯ![]() µДЖХНЁ·ЅіМУлЗъПЯ
µДЖХНЁ·ЅіМУлЗъПЯ![]() µДЦ±ЅЗЧш±к·ЅіМЈ»
µДЦ±ЅЗЧш±к·ЅіМЈ»
ЈЁ2Ј©Йиµг![]() .ИфЦ±
.ИфЦ±![]() УлЗъПЯ
УлЗъПЯ![]() ПаЅ»УЪБЅµг
ПаЅ»УЪБЅµг![]() ,Зу
,Зу![]() µДЦµ.
µДЦµ.
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com