
【题目】如图,已知四棱锥![]() 的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.
的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.
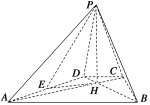
(1)证明:PE⊥BC;
(2)若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.
【答案】(1)见解析(2)![]()
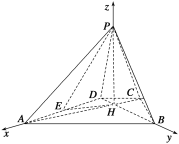
【解析】(1)证明:以H为原点,HA,HB,HP所在直线分别为x,y,z轴建立空间直角坐标系,如图,设![]() ,
,![]() ,
,![]() ,则A(1,0,0),B(0,1,0),
,则A(1,0,0),B(0,1,0),
C(-m, 0, 0),P(0, 0,n),D(0,-m, 0),E(![]() ,
,![]() ,0),可得
,0),可得![]() =(
=(![]() ,
,![]() ,-n),
,-n),![]() =(-m,-1, 0).
=(-m,-1, 0).
因为![]() ·
·![]() =
=![]() +
+![]() +0=0,所以PE⊥BC.
+0=0,所以PE⊥BC.
(2)由已知条件可得m=![]() ,n=1,故C(-
,n=1,故C(-![]() ,0, 0),D(0,-
,0, 0),D(0,-![]() ,0),
,0),
E(![]() ,-
,-![]() ,0),P(0, 0, 1),则
,0),P(0, 0, 1),则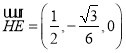 ,
,![]() ,
,
设![]() =(x,y,z)为平面PEH的法向量,
=(x,y,z)为平面PEH的法向量,
则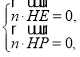 即
即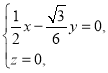 因此可以取
因此可以取![]() =(1,
=(1,![]() ,0),
,0),
又![]() =(1, 0,-1),所以|cos〈
=(1, 0,-1),所以|cos〈![]() ,
,![]() 〉|=
〉|=![]() ,
,
所以直线PA与平面PEH所成角的正弦值为![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx和g(x)=lnx. (Ⅰ) 若a=b=1,求证:f(x)的图象在g(x)图象的上方;
(Ⅱ) 若f(x)和g(x)的图象有公共点P,且在点P处的切线相同,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
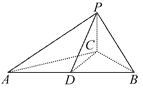
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=logax(a>0且a≠1)的图象过点(4,2),
(1)求a的值.
(2)若g(x)=f(1-x)+f(1+x),求g(x)的解析式及定义域.
(3)在(2)的条件下,求g(x)的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c的图象过点(﹣1,3),且关于直线x=1对称
(Ⅰ)求f(x)的解析式;
(Ⅱ)若m<3,求函数f(x)在区间[m,3]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点. 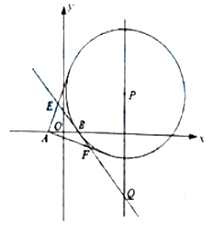
(1)求证:|EA|+|EB|为定值;
(2)证明:设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com