
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)若对任意的![]() ,都有
,都有![]() 成立,求a的取值范围.
成立,求a的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)当
(Ⅱ)当![]() 时增区间为
时增区间为![]() 当
当![]() 时增区间为
时增区间为![]() ,减区间为
,减区间为![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题(Ⅰ)利用导数的几何意义得到切线的斜率,进而得到切线方程(Ⅱ)首先计算函数的导数,令导数大于零可得增区间,进而得到减区间,求解时注意对参数的取值范围分情况讨论(Ⅲ)不等式恒成立问题中求参数范围的一般采用分离参数的方法,转化为求函数的最值问题
试题解析:(Ⅰ)![]() 时,
时,![]()
![]()
曲线![]() 在点
在点![]() 处的切线方程
处的切线方程![]()
(Ⅱ)![]()
①当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 的递增区间为
的递增区间为![]()
②当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]()
x | ( 0, |
| ( |
f’(x) | - | + | |
f(x) | 减 | 增 |
所以函数![]() 的递增区间为
的递增区间为![]() ,递减区间为
,递减区间为![]()
(Ⅲ)对任意的![]() ,使
,使![]() 成立,只需任意的
成立,只需任意的![]() ,
,![]()
①当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
所以只需![]()
而![]()
所以![]() 满足题意;
满足题意;
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
所以只需![]()
而![]()
所以![]() 满足题意;
满足题意;
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数,
上是减函数,![]() 上是增函数,
上是增函数,
所以只需![]() 即可
即可
而![]()
从而![]() 不满足题意;
不满足题意;
综合①②③实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 的焦点在
的焦点在![]() 轴上,A是E的左顶点,斜率为k (k > 0)的直线交E于A,M两点,点N在E上,MA⊥NA.
轴上,A是E的左顶点,斜率为k (k > 0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,![]() 时,求△AMN的面积;
时,求△AMN的面积;
(Ⅱ)当![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A. ![]() ,使得
,使得![]() 成立.
成立.
B. 命题![]() :任意
:任意![]() ,都有
,都有![]() ,则
,则![]() :存在
:存在![]() ,使得
,使得![]() .
.
C. 命题“若![]() 且
且![]() ,则
,则![]() 且
且![]() ”的逆命题为真命题.
”的逆命题为真命题.
D. 若数列![]() 是等比数列,
是等比数列,![]() 则
则![]() 是
是![]() 的必要不充分条件.
的必要不充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 的两顶点
的两顶点![]() ,且点
,且点![]() 满足
满足![]()
(1)求动点![]() 的轨迹方程;
的轨迹方程;![]()
(2)设![]() ,求动点
,求动点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,过点
,过点![]() 作
作![]() 轴垂线
轴垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程,否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程,否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老师是省级课题组的成员,主要研究课堂教学目标达成度,为方便研究,从实验班中随机抽取30次的随堂测试成绩进行数据分析.已知学生甲的30次随堂测试成绩如下(满分为100分):
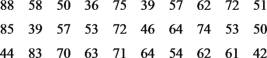
(1)把学生甲的成绩按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,列出频率分布表,并画出频率分布直方图:
分成6组,列出频率分布表,并画出频率分布直方图:
(2)为更好的分析学生甲存在的问题,从随堂测试成绩50分以下(不包括50分)的试卷中随机抽取3份进行分析,求恰有2份成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
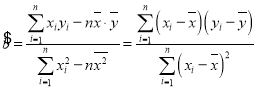 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com