
| A. | $\frac{5-\sqrt{7}}{3}$ | B. | $\frac{5+\sqrt{7}}{3}$ | C. | $\frac{7-\sqrt{5}}{3}$ | D. | $\frac{7+\sqrt{5}}{3}$ |
分析 长方体盒子的长为(6-2x),宽为(4-2x),高为x,容积V=(6-2x)(4-2x)x=4x3-20x2+24x,由此利用导数性质能求出要使容积最大的x值.
解答 解:长方体盒子的长为(6-2x),宽为(4-2x),高为x,
由于盒子的长宽高都为正数,所以6-2x>0,4-2x>0,x>0,解得0<x<2
所以容积V=(6-2x)(4-2x)x=4x3-20x2+24x
要求V的最大值,求V的导数,并求导数的零点
V'=12x2-40x+24,令V'=0,解得x=$\frac{5±\sqrt{7}}{3}$,
由于0<x<2,所以取x=$\frac{5-\sqrt{7}}{3}$,
由于V'是开口向上的二次函数,x=$\frac{5-\sqrt{7}}{3}$是其左零点
所以当x<$\frac{5-\sqrt{7}}{3}$时,V'>0;x>$\frac{5-\sqrt{7}}{3}$时,V'<0,
即当x=$\frac{5-\sqrt{7}}{3}$时,V有极大值
∴要使容积最大,x=$\frac{5-\sqrt{3}}{3}$.
故选:A.
点评 本题考查正方形有边长的求法,考查长方体的体积的求法及应用,考查推理论证能力、运算求解能力、空间思维能力、空间想象能力,考查转化化归思想、数形结合思想,是中档题.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 由a的取值确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [一1,2] | B. | (一1,2] | C. | [2,+∞) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | $({\frac{1}{2},\frac{1}{4}})$ | C. | $({\frac{1}{3},\frac{1}{9}})$ | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
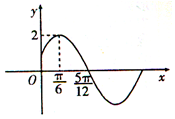 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com