
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别在线段
分别在线段![]() 和
和![]() 上,且
上,且![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.
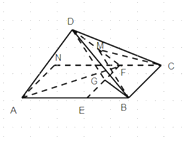
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 为线段
为线段![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见详解;(2)![]() .
.
【解析】
(1)先证![]() ,再由面面垂直推证
,再由面面垂直推证![]() 平面
平面![]() ,即可由线面垂直推证面面垂直;
,即可由线面垂直推证面面垂直;
(2)将问题转化为求![]() 的体积,结合几何关系,即可容易求得结果.
的体积,结合几何关系,即可容易求得结果.
(1)延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于
于![]() ,四边形
,四边形![]() 如下图所示:
如下图所示:

因为![]() ,故可得
,故可得![]() ,
,
故可得![]() ,
,
又因为![]() ,
,
则![]() ,
,
在![]() 中,
中,![]() ,
,
故可得![]() ,
,
因为平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
又因为![]() 平面
平面![]() ,
,
故可得![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
故可得平面![]() 平面
平面![]() .即证.
.即证.
(2)因为![]() 为
为![]() 中点,
中点,
故![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 距离的
距离的![]() ;
;
又因为![]() //
//![]() ,
,![]() 平面
平面![]() ,
,
故![]() //平面
//平面![]() ,
,
则点![]() 到平面
到平面![]() 的距离与
的距离与![]() 到平面
到平面![]() 的距离相等.
的距离相等.
故![]() .
.
取![]() 中点为
中点为![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
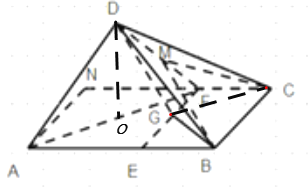
因为![]() ,故可得
,故可得![]() ,
,
又因为平面![]() 平面
平面![]() ,且交于
,且交于![]() ,
,
![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() .
.
即![]() 为
为![]() 到平面
到平面![]() 的距离.
的距离.
又因为![]() ,
,![]() ,
,
故![]() .
.
在![]() 中,因为
中,因为![]() ,
,![]() ,
,
故![]() ,解得
,解得![]() .
.
故![]() .
.
即三棱锥![]() 的体积为
的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两工人在同样的条件下生产,日产量相等,每天出废品的情况如下表:

则下列结论中正确的是 ( )
A. 甲生产的产品质量比乙生产的产品质量好一些
B. 乙生产的产品质量比甲生产的产品质量好一些
C. 两人生产的产品质量一样好
D. 无法判断谁生产的产品质量好一些
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生对《3.12植树节》活动节日的相关内容,学校进行了一次10道题的问卷调查,从该校学生中随机抽取50人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五组,得到如下频率分布直方图.
五组,得到如下频率分布直方图.
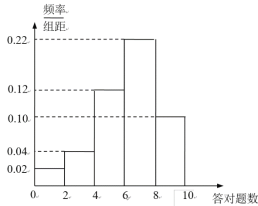
(1)若答对一题得10分,答错和未答不得分,估计这50名学生成绩的平均分;
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD中,底面ABCD是边长为2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值为
,二面角S-BD-C的余弦值为![]() .
.
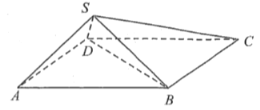
(I)证明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥的顶点为A,高和底面的半径相等,BE是底面圆的一条直径,点D为底面圆周上的一点,且∠ABD=60°,则异面直线AB与DE所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
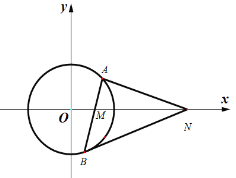
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方),问在
轴上方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com