
【题目】已知函数f(x)=ex+ax,(a∈R),其图象与x轴交于A(x1 , 0),B(x2 , 0)两点,且x1<x2
(1)求a的取值范围;
(2)证明: ![]() ;(f′(x)为f(x)的导函数)
;(f′(x)为f(x)的导函数)
(3)设点C在函数f(x)的图象上,且△ABC为等边三角形,记 ![]() ,求(t﹣1)(a+
,求(t﹣1)(a+ ![]() )的值.
)的值.
【答案】
(1)解:∵f(x)=ex+ax,∴f'(x)=ex+a,
若a≥0,则f'(x)>0,则函数f(x)在R上单调递增,这与题设矛盾.
∴a<0,
令f′(x)>0得x>ln(﹣a),令f′(x)<0得x<ln(﹣a),
∴f(x)在(﹣∞,ln(﹣a))上单调递减,在(ln(﹣a),+∞)上单调递增,
∴f(x)有两个零点,
∴fmin(x)=f(ln(﹣a))=﹣a+aln(﹣a),
∴﹣a+aln(﹣a)<0,解得a<﹣e.
(2)解:证明:∵x1,x2是f(x)的零点,∴ 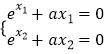 ,
,
两式相减得:a=﹣ ![]() .
.
记 ![]() =s,则f′(
=s,则f′( ![]() )=e
)=e ![]() ﹣
﹣ ![]() =
= ![]() [2s﹣(es﹣e﹣s)],
[2s﹣(es﹣e﹣s)],
设g(s)=2s﹣(es﹣e﹣s),则g′(s)=2﹣(es+e﹣s)<0,
∴g(s)是减函数,
∴g(s)<g(0)=0,
又 ![]() >0,∴f′(
>0,∴f′( ![]() )<0.
)<0.
∵f′(x)=ex+a是增函数,
∴f′( ![]() )<f′(
)<f′( ![]() )<0
)<0
(3)解:由 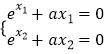 得
得 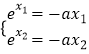 ,∴e
,∴e ![]() =﹣a
=﹣a ![]() ,
,
设P(x0,y0),在等边三角形ABC中,易知 ![]() ,y0=f(x0)<0,
,y0=f(x0)<0,
由等边三角形性质知y0=﹣ ![]() ,∴y0+
,∴y0+ ![]() =0,即
=0,即 ![]() ,
,
∴﹣a ![]() +
+ ![]() (x1+x2)+
(x1+x2)+ ![]() =0,
=0,
∵x1>0,∴  ,
,
∴﹣at+ ![]() (t2+1)+
(t2+1)+ ![]() (t2﹣1)=0,即(a+
(t2﹣1)=0,即(a+ ![]() )t2﹣2at+a﹣
)t2﹣2at+a﹣ ![]() =0,
=0,
∴[(a+ ![]() )t+
)t+ ![]() ](t﹣1)=0,
](t﹣1)=0,
∵t>1,∴(a+ ![]() )t+
)t+ ![]() =0,
=0,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)讨论a的符号,判断f(x)的单调性,计算f(x)的极值,根据零点个数得出f(x)的极小值为负数,列出不等式解出a;(2)计算f′( ![]() ),根据函数单调性判断f′(
),根据函数单调性判断f′( ![]() )的符号,根据f′(x)的单调性得出结论;(3)用x1 , x2表示出P点坐标,根据等边三角形的性质列方程化简即可求出t和a的关系,再计算(t﹣1)(a+
)的符号,根据f′(x)的单调性得出结论;(3)用x1 , x2表示出P点坐标,根据等边三角形的性质列方程化简即可求出t和a的关系,再计算(t﹣1)(a+ ![]() )的值.
)的值.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:![]() )的分组区间为
)的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将其按从左到右的顺序分别编号为第一组,第二组,
,将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.
,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1,2,3,4,5的五个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和与标号之积都不小于5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 ![]() 轴的正半轴,建立平面直角坐标系,在平面直角坐标系
轴的正半轴,建立平面直角坐标系,在平面直角坐标系 ![]() 中,直线
中,直线 ![]() 经过点
经过点 ![]() ,倾斜角
,倾斜角 ![]() .
.
(1)写出曲线 ![]() 的直角坐标方程和直线
的直角坐标方程和直线 ![]() 的参数方程;
的参数方程;
(2)设 ![]() 与曲线
与曲线 ![]() 相交于
相交于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)![]() 表示开始第4次发球时乙的得分,求
表示开始第4次发球时乙的得分,求 ![]() 的期望.
的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com