
分析 (1)根据题意表示出|OA|与|OB|,以及|OC|,代入已知等式求出λ的值即可;
(2)根据φ的度数,表示出B与C的极坐标,转化为直角坐标,根据C是经过点(m,0)且倾斜角为α的直线,确定出经过B,C的直线方程,求出m与α的值.
解答 解:(1)根据题意得:|OA|=4cosφ,|OB|=4cos(φ+$\frac{π}{4}$),|OC|=4cos(φ-$\frac{π}{4}$),
则|OB|+|OC|=4cos(φ+$\frac{π}{4}$)+4cos(φ-$\frac{π}{4}$)=2$\sqrt{2}$(cosφ-sinφ)+2$\sqrt{2}$(cosφ+sinφ)=4$\sqrt{2}$cosφ=$\sqrt{2}$|OA|,
∴λ=$\sqrt{2}$;
(2)当φ=$\frac{π}{12}$时,B,C两点的极坐标分别为(2,$\frac{π}{3}$),(2$\sqrt{3}$,-$\frac{π}{6}$)化为直角坐标为B(1,$\sqrt{3}$),C(3,-$\sqrt{3}$),
∵C是经过点(m,0)且倾斜角为α的直线,且经过B,C的直线方程为y=-$\sqrt{3}$(x-2),
∴m=2,α=$\frac{2π}{3}$.
点评 此题考查了参数方程化为普通方程,以及简单曲线的极坐标方程,熟练掌握各坐标之间的转化是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
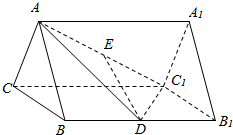 在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.
在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{47}{32}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com