
分析 由题意作出平面区域,而且(x-2)2+(y-1)2的几何意义是点A(2,1)与阴影内的点的距离的平方,从而解得.
解答 解:由题意作平面区域如下,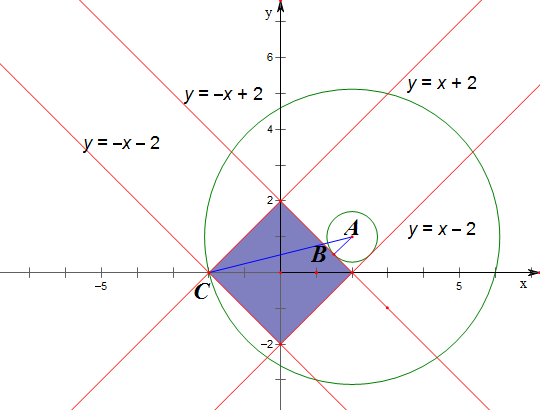
(x-2)2+(y-1)2的几何意义是点A(2,1)与阴影内的点的距离的平方,
易知|AB|=$\frac{|2+1-2|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,|AC|=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
故(x-2)2+(y-1)2的最小值为$(\frac{\sqrt{2}}{2})^{2}$=$\frac{1}{2}$,(x-2)2+(y-1)2的最大值为$(\sqrt{17})^{2}$=17,
故(x-2)2+(y-1)2的最小值与最大值之和为$\frac{35}{2}$,
故答案为:$\frac{35}{2}$.
点评 本题考查了线性规划的变形应用及圆的定义与应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com