练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知集合A={-1，1}，B={∅，{-1}，{1}，{-1，1}}，则A与B的关系是（　　）
    A．A⊆BB．A∈BC．A与B无关系D．A?B

    分析 由已知可得集合B的每个元素均为一个集合，进而可得A，B的关系．

    解答 解：∵集合A={-1，1}，B={∅，{-1}，{1}，{-1，1}}，
    ∴A∈B，
    故选：B．

    点评 本题考查的知识点是集合的表示法，元素与集合的关系，难度不大，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

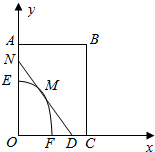    13．如图，某小区有一矩形地块OABC，其中OC=2，OA=3，单位：百米．已知 O EF是一个游泳池，计划在地块OABC内修一条与池边 EF相切于点 M的直路l（宽度不计），交线段OC于点D，交线段OA于点 N．现以点 O为坐标原点，以线段 OC所在直线为x轴，建立平面直角坐标系，若池边 EF满足函数y=-x2+2（$0≤x≤\sqrt{2}$）的图象．若点 M到y轴距离记为t．
    （1）当$t=\frac{2}{3}$时，求直路l所在的直线方程；
    （2）当t为何值时，地块OABC在直路l不含泳池那侧的面积取到最大，最大值时多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．己知抛物线C1：x2=2py（p＞0）与圆C2：x2+y2=5的两个交点之间的距离为4．
    （Ⅰ）求p的值；
    （Ⅱ）设过抛物线C1的焦点F且斜率为k的直线与抛物线交于A，B两点，与圆C2交于C，D两点，当k∈[0，1]时，求|AB|•|CD|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．对于在区间[m，n]上有意义的两个函数f（x）和g（x），如果对于任意的x∈[m，n]，都有|f（x）-g（x）|≤1恒成立，则称f（x）与g（x）在区间[m，n]上是接近的，否则称f（x）与g（x）在[m，n]上是非接近的，现有函数f1（x）=loga（x-3a），f2（x）=loga$\frac{1}{x-a}$（a＞0，a≠1）给定一个区间[a+2，a+3]．
    （1）当a=$\frac{1}{2}$时，判断f1（x）与f2（（x）在区间[a+2，a+3]上是否是接近的，并说明理由；
    （2）若f1（x）与f2（x）在区间[a+2，a+3]上是接近的，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．四棱锥P-ABCD中，CD∥AB，CD=2AB，E为PC中点，R为CD中点．
    （1）求证：平面BER∥面PAD；
    （2）若BE=AD=4，PA=4$\sqrt{3}$，求异面直线BE与DA所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．设集合A={x|-3＜2x+1＜11}，B={x|x＜a}，A∩B≠∅，则a的取值范围是a＞-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知集合A={x|x2-3x+2=0}，B={x|x2-ax+2=0}．问满足A∪B=A的实数a是否存在？若存在，求出a的值；若不存在，请说明理由！

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

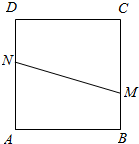    12．如图，边长为1正方形ABCD中，分别在边BC、AD上各取一点M与N，下面用随机模拟的方法计算|MN|＞1.1的概率．利用计算机中的随机函数产生两个0～1之间的随机实数x，y，设BM=x，AN=y，则可确定M、N点的位置，进而计算线段MN的长度．设x，y组成数对（x，y），经随机模拟产生了20组随机数：
    （0.82，0.28）（0.47，0.38）（0.71，0.62）（0.68，0.83）（0.66，0.63）
    （0.66，0.18）（0.01，0.35）（0.59，0.06）（0.28，0.22）（0.27，0.05）
    （0.98，0.32）（0.92，0.99）（0.70，0.49）（0.38，0.60）（0.06，0.78）
    （0.24，0.46）（0.17，0.75）（0.77，0.59）（0.15，0.98）（0.63，0.78）
    通过以上模拟数据，可得到“|MN|＞1.1”的概率是（　　）
    A．0.3B．0.35C．0.65D．0.7

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．数列{an}中，a1=1，a2=2，an+2=an+1-an，则{an}的前2015项和S2015=1．

    查看答案和解析>>

    同步练习册答案