
【题目】有一个由0和1构成的6行n列的 数字方阵,其中每行中恰有5个1,任意两行中同一列都取1的列数不超过2.求n的 最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区![]() 名居民参加
名居民参加![]() 年国庆活动,他们的年龄在
年国庆活动,他们的年龄在![]() 岁至
岁至![]() 岁之间,将年龄按
岁之间,将年龄按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到的频率分布直方图如图所示.
分组,得到的频率分布直方图如图所示.
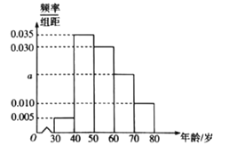
(1)求![]() 的值,并求该社区参加
的值,并求该社区参加![]() 年国庆活动的居民的平均年龄(每个分组取中间值作代表);
年国庆活动的居民的平均年龄(每个分组取中间值作代表);
(2)现从年龄在![]() 、
、![]() 的人员中按分层抽样的方法抽取
的人员中按分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行座谈,用
人进行座谈,用![]() 表示参与座谈的居民的年龄在
表示参与座谈的居民的年龄在![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若用样本的频率代替概率,用随机抽样的方法从该地![]() 岁至
岁至![]() 岁之间的市民中抽取
岁之间的市民中抽取![]() 名进行调查,其中有
名进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() ,当
,当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西北某省会城市计划新修一座城市运动公园,设计平面如图所示:其为五边形![]() ,其中三角形区域
,其中三角形区域![]() 为球类活动场所;四边形
为球类活动场所;四边形![]() 为文艺活动场所,
为文艺活动场所,![]() ,为运动小道(不考虑宽度)
,为运动小道(不考虑宽度)![]() ,
,![]() ,
,![]() 千米.
千米.

(1)求小道![]() 的长度;
的长度;
(2)求球类活动场所![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回答下列两个问题, 并给出例子或证明.
(1)对任意正整数![]() , 在平面上是否都存在
, 在平面上是否都存在![]() 个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
个不在同一条直线上的点, 使得任意两点间的距离都为正整数?
(2)在平面上是否存在两两不同的无限点列组成的点集![]() , 使得
, 使得![]() 内所有点不在同一条直线上, 且
内所有点不在同一条直线上, 且![]() 内任意两点间的距离为正整数?
内任意两点间的距离为正整数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com