解:(1)证:∵

=

(
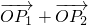
),
∴P是P
1P
2的中点?x
1+x
2=1------(2分)
∴y
1+y
2=f(x
1)+f(x
2)=
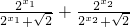
=
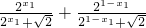
=
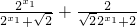
=1.
∴
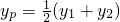
=

..-----------------------------(4分)
(2)解:由(1)知x
1+x
2=1,f (x
1)+f (x
2)=y
1+y
2=1,f (1)=2-

,
S
n=f(

)+f(

)+…+f(

)+f(
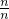
),
S
n=f(
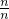
)+f(

)+…+f(

)+f(

),
相加得 2S
n=f(1)+[f(

)+f(

)]+[f(

)+f(
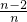
)]+…+[f(

)+f(

)]+f(1),
=2f(1)+n-1=n+3-2

∴
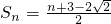
.------------(8分)
(3)解:
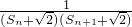
=
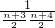
=
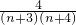
=
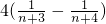
,
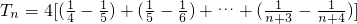
--------------------(10分)
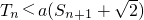
?a
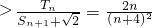
=
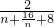
∵
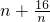
≥8,当且仅当n=4时,取“=”
∴
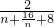
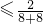
=

,因此,a
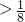
-------------------(12分)
分析:(1)由于点在函数图象上,同时满足

=

(
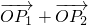
),那么利用坐标化简得到结论.
(2)根据f (x
1)+f (x
2)=y
1+y
2=1,f (1)=2-

,结合倒序相加法求解得到结论.
(3)根据已知的和式得到
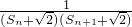
=
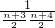
=
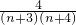
=
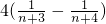
,裂项求和的数学思想得到证明.
点评:本试题主要考查了函数,与向量,以及数列的知识的综合运用.以函数为模型,确定点的坐标关系式,进一步结合向量得到结论,并利用倒序相加法求解和,同时利用裂项求和得到不等式的证明.

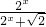 的图象上两点P1(x1,y1)、P2(x2,y2),若
的图象上两点P1(x1,y1)、P2(x2,y2),若 =
= (
(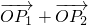 ),且点P的横坐标为
),且点P的横坐标为 .
. )+f(
)+f( )+A+f(
)+A+f( )+f(
)+f(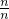 )
)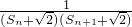 }的前n项和,若Tn<a(Sn+1+
}的前n项和,若Tn<a(Sn+1+ )对一切n∈N*都成立,试求a的取值范围.
)对一切n∈N*都成立,试求a的取值范围. =
= (
(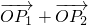 ),
),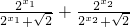 =
=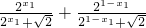 =
=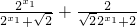 =1.
=1.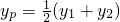 =
= ..-----------------------------(4分)
..-----------------------------(4分) ,
, )+f(
)+f( )+…+f(
)+…+f( )+f(
)+f(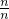 ),
),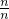 )+f(
)+f( )+…+f(
)+…+f( )+f(
)+f( ),
), )+f(
)+f( )]+[f(
)]+[f( )+f(
)+f(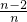 )]+…+[f(
)]+…+[f( )+f(
)+f( )]+f(1),
)]+f(1),
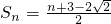 .------------(8分)
.------------(8分)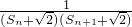 =
=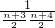 =
=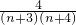 =
=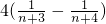 ,
,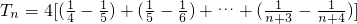 --------------------(10分)
--------------------(10分) 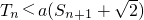 ?a
?a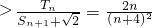 =
=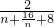
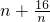 ≥8,当且仅当n=4时,取“=”
≥8,当且仅当n=4时,取“=”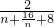
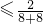 =
= ,因此,a
,因此,a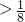 -------------------(12分)
-------------------(12分) =
= (
(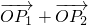 ),那么利用坐标化简得到结论.
),那么利用坐标化简得到结论. ,结合倒序相加法求解得到结论.
,结合倒序相加法求解得到结论.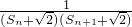 =
=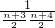 =
=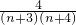 =
=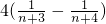 ,裂项求和的数学思想得到证明.
,裂项求和的数学思想得到证明.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案