
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
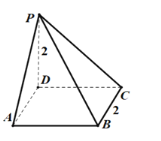
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
【答案】(1) S=8+4![]() ,,V=
,,V=![]() (2) (24-16
(2) (24-16![]() )π.
)π.
【解析】
(1) 四个侧面都是直角三角形,进而求出边长,即可求得侧面积,底面是正方形,二者相加即可求出表面积,PD⊥平面ABCD,故四棱锥的高为![]() ,再由棱锥的体积公式求出体积;
,再由棱锥的体积公式求出体积;
(2) 设内切球的半径为r,球心为O,根据等体积法求出内切球的半径,则由![]() 即可求得半径,进而求出内切球的表面积.
即可求得半径,进而求出内切球的表面积.
(1) 解:(1)由已知底面ABCD为正方形,PD⊥平面ABCD,
![]() ,得PD⊥AD,PD⊥AB,AD⊥AB.
,得PD⊥AD,PD⊥AB,AD⊥AB.
又![]() ,∴AB⊥平面PAD,∴PA⊥AB,∴PA
,∴AB⊥平面PAD,∴PA⊥AB,∴PA![]() PB
PB![]()
∴![]()
![]()
同理![]()
![]()
![]()
∴![]()
![]() .
.
S=8+4![]() ,,V=
,,V=![]()
(2)设内切球的半径为r,球心为O,
则球心O到平面PAB,平面PAD,平面PCB,平面PCD,平面ABCD的距离均为r,
由![]() 可得
可得
![]()
∴![]()
∴![]() .
.
∴r=2-![]() ,S=(24-16
,S=(24-16![]() )π.
)π.


科目:高中数学 来源: 题型:
【题目】已知关于x的不等式(4kx﹣k2﹣12k﹣9)(2x﹣11)>0,其中k∈R,对于不等式的解集A,记B=A∩Z(其中Z为整数集),若集合B是有限集,则使得集合B中元素个数最少时的实数k的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数m,使得
,若存在实数m,使得![]() 为R上的奇函数,则称
为R上的奇函数,则称![]() 是位差值为m的“位差奇函数”.
是位差值为m的“位差奇函数”.
(1)判断函数![]() 和
和![]() 是否是位差奇函数,并说明理由;
是否是位差奇函数,并说明理由;
(2)若![]() 是位差值为
是位差值为![]() 的位差奇函数,求
的位差奇函数,求![]() 的值;
的值;
(3)若对于任意![]() ,
,![]() 都不是位差值为m的位差奇函数,求实数t的取值范围.
都不是位差值为m的位差奇函数,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 是函数
是函数![]() 的反函数,解方程
的反函数,解方程![]() ;
;
(2)当![]()
![]() 时,定义
时,定义![]() ,设
,设![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,求
,求![]() 及
及![]() ;
;
(3)对于任意![]() ,其中
,其中![]() ,当
,当![]() 能作为一个三角形的三边长时,
能作为一个三角形的三边长时,![]() 也总能作为一个三角形的三边长,试探究M的最小值.
也总能作为一个三角形的三边长,试探究M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分,某考试每道都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道能排除两个错误选项,另2题只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机挑选一个选项做答,且各题做答互不影响.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,焦距为
,焦距为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为弦
为弦![]() 的中点.
的中点.
(1)求椭圆的标准方程;
(2)若直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() ,若
,若![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
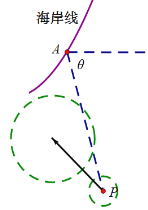
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市A(看做一点)的东偏南![]() 角方向
角方向![]() ,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
(1) 问10小时后,该台风是否开始侵袭城市A,并说明理由;
(2) 城市A受到该台风侵袭的持续时间为多久?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与直线
与直线![]() 有且只有一个交点,点P为椭圆C上任一点,
有且只有一个交点,点P为椭圆C上任一点,![]() ,
,![]() .若
.若![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线![]() 与椭圆C交于不同两点A,B,点O为坐标原点,且
与椭圆C交于不同两点A,B,点O为坐标原点,且![]() ,当
,当![]() 的面积S最大时,求
的面积S最大时,求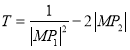 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: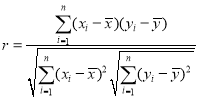 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com