
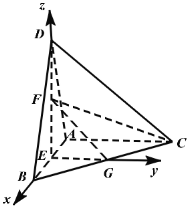
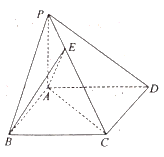
【题目】如图,三棱锥![]() 中,
中,![]() ,
,![]() 是正三角形,且平面
是正三角形,且平面![]() 平面ABC,
平面ABC,![]() ,E,G分别为AB,BC的中点.
,E,G分别为AB,BC的中点.

(Ⅰ)证明:![]() 平面ABD;
平面ABD;
(Ⅱ)若F是线段DE的中点,求AC与平面FGC所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)由题可得![]() ,又可证
,又可证![]() 平面ABD,从而可证
平面ABD,从而可证![]() 平面ABD;
平面ABD;
(Ⅱ)以E为坐标原点,建立如图所示的空间直角坐标系![]() ,利用向量法求解AC与平面FGC所成角的正弦值.
,利用向量法求解AC与平面FGC所成角的正弦值.
(Ⅰ)因为E,G分别为AB,BC的中点,所以![]() .
.
因为![]() ,平面
,平面![]() 平面ABC,
平面ABC,
平面![]() 平面
平面![]() ,
,
所以![]() 平面ABD,
平面ABD,
所以![]() 平面ABD;
平面ABD;
(Ⅱ)因为![]() 是正三角形,所以
是正三角形,所以![]() .
.
又由(Ⅰ)知![]() 平面ABD,即EG,AB,DE两两垂直,
平面ABD,即EG,AB,DE两两垂直,
则以E为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为
x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系![]() .
.
因为![]() ,
,![]() 是正三角形,
是正三角形,
所以![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
因为F是DE的中点,所以![]() .
.
![]() ,
,![]() ,
,![]() .
.
设平面FGC的一个法向量为![]() ,
,
所以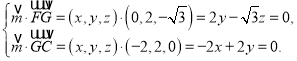
令![]() ,则
,则![]() ,
,![]() ,所以
,所以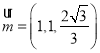 .
.
设AC与平面FGC所成的角为![]() ,
,
则 .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 为正项等比数列,
为正项等比数列,![]() 为
为![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)从三个条件:①![]() ;②
;②![]() ;③
;③![]() 中任选一个作为已知条件,求数列
中任选一个作为已知条件,求数列![]() 的前
的前![]() 项和
项和![]() .
.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递增,下述三个结论:①
单调递增,下述三个结论:①![]() 的取值范围是
的取值范围是![]() ;②
;②![]() 在
在![]() 存在零点;③
存在零点;③![]() 在
在![]() 至多有4个极值点.其中所有正确结论的编号是( )
至多有4个极值点.其中所有正确结论的编号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右准线为直线
的右准线为直线![]() ,左顶点为
,左顶点为![]() ,右焦点为
,右焦点为![]() . 已知斜率为2的直线
. 已知斜率为2的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 到直线
到直线![]() 的距离为
的距离为![]()
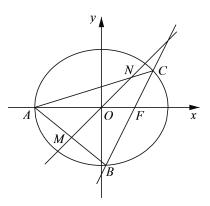
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的直线
的直线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:6月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,
为平行四边形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)在侧棱![]() 上是否存在点E,使
上是否存在点E,使![]() 与底面
与底面![]() 所成的角为45°?若存在,求
所成的角为45°?若存在,求![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答所提问题:设函数![]() ,①
,①![]() 的定义域为
的定义域为![]() ,其图像是一条连续不断的曲线;②
,其图像是一条连续不断的曲线;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 上不是单调函数;④
上不是单调函数;④![]() 恰有
恰有![]() 个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com