
分析 (Ⅰ)利用an+1=Sn+1-Sn可知$\frac{{a}_{n+1}+2}{{a}_{n}+2}$=2(n≥2),进而可得结论;
(Ⅱ)通过(Ⅰ)可知an=3•2n-1-2,进而计算即得结论.
解答 (Ⅰ)证明:当n≥2时,∵Sn+1=2Sn+2n+1(n∈N*),
∴an+1=Sn+1-Sn=(2Sn+2n+1)-(2Sn-1+2n-1)=2an+2,
∴an+1+2=2(an+1),
即$\frac{{a}_{n+1}+2}{{a}_{n}+2}$=2(n≥2),
∵a1=1,
∴a1+a2=2a1+3,
∴a2=a1+3=4,
∴a1+2=3,a2+2=6,
∴$\frac{{a}_{2}+2}{{a}_{1}+2}$=$\frac{6}{3}$=2,
∴数列{an+2}是以3为首项,2为公比的等比数列;
(Ⅱ)解:由(Ⅰ)知an+2=3•2n-1,
∴an=3•2n-1-2,
∴Sn=3(1+2+22+…+2n-1)-2n
=$3•\frac{1-{2}^{n}}{1-2}$-2n
=3•2n-2n-3.
点评 本题考查等比数列的判定、数列的前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | 17 | 12 | 7 | 4 |
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b>0 | D. | a<0,b>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )
在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
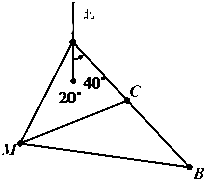 如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?
如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com