
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 附:K2= ![]()
P(K2>k0) | 0.10 | 0.05 |
| 0.005 |
k0 | 2.706 | 3.841 |
| 7.879 |
【答案】
(1)解:将2×2列联表中的数据代入公式,计算得
x2= ![]() =
= ![]() ≈4.762,
≈4.762,
因为4.762>3.841,
所以有95%的把握认为南方学生和北方学生在选用甜品的饮食习惯方面有差异
(2)解:这5名数学系学生中,2名喜欢甜品的记为A、B,
其余3名不喜欢甜品的学生记为c、d、e,
则从这5名学生中任取3人的结果所组成的基本事件为
ABc,ABd,ABe,Acd,Ace,Ade,Bcd,Bce,Bde,cde,共10种;
3人中至多有1人喜欢甜品的基本事件是
Acd,Ace,Ade,Bcd,Bce,Bde,cde,共7种;
所以,至多有1人喜欢甜品的概率为P= ![]()
【解析】(1)利用2×2列联表中的数据计算观测值x2,对照表中数据即可得出结论;(2)利用列举法求出从这5名学生中任取3人的基本事件数,计算对应的概率即可.


科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项都是正数,2a5 , a4 , 4a6成等差数列,且满足 ![]() ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ![]() ,n∈N* , 且b1=1
,n∈N* , 且b1=1
(1)求数列{an},{bn}的通项公式
(2)设 ![]() ,n∈N* , {Cn}前n项和为
,n∈N* , {Cn}前n项和为 ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为角A,B,C所对的边.已知sinC= ![]() sinB,c=2,cosA=
sinB,c=2,cosA= ![]() .
.
(Ⅰ)求a的值;
(Ⅱ)求sin(2A﹣ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,随机抽取了6个试销售数据,得到第i个销售单价xi(单位:元)与销售yi(单位:件)的数据资料,算得 ![]()
(1)求回归直线方程 ![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本)
附:回归直线方程 ![]() 中,
中, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中
,其中 ![]() ,
, ![]() 是样本平均值.
是样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)将直线l: 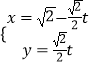 (t为参数)化为极坐标方程;
(t为参数)化为极坐标方程;
(2)设P是(1)中直线l上的动点,定点A( ![]() ,
, ![]() ),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,记抛物线y=x﹣x2与x轴所围成的平面区域为M,该抛物线与直线y=kx(k>0)所围成的平面区域为N,向区域M内随机抛掷一点P,若点P落在区域N内的概率为 ![]() ,则k的值为( )
,则k的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的偶函数,且f(2+x)=f(2﹣x),当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6)内关于x的方程f(x)﹣log a(x+2)=0,恰有4个不同的实数根,则实数a(a>0,a≠1)的取值范围是( )
)x﹣1,若在区间(﹣2,6)内关于x的方程f(x)﹣log a(x+2)=0,恰有4个不同的实数根,则实数a(a>0,a≠1)的取值范围是( )
A.( ![]() ,1)
,1)
B.(1,4)
C.(1,8)
D.(8,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com