
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况,![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
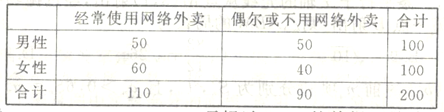
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

【答案】(1)不能在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖情况与性别有关.
市使用网络外卖情况与性别有关.
(2)①![]() ;②
;②![]() ;
;![]() .
.
【解析】试题分析:(1)计算![]() 的值,进而可查表下结论;
的值,进而可查表下结论;
(2)①由分层抽样的抽样比计算即可;
②由![]() 列联表,可知抽到经常使用网络外卖的网民的频率为
列联表,可知抽到经常使用网络外卖的网民的频率为![]() ,将频率视为概率,即从
,将频率视为概率,即从![]() 市市民中任意抽取1人,恰好抽到经常使用网络外卖的市民的概率为
市市民中任意抽取1人,恰好抽到经常使用网络外卖的市民的概率为![]() ,由题意得
,由题意得![]() .
.
试题解析:
(1)由列联表可知![]() 的观测值,
的观测值,![]()
![]() .
.
所以不能在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖情况与性别有关.
市使用网络外卖情况与性别有关.
(2)①依题意,可知所抽取的5名女网民中,经常使用网络外卖的有![]() (人),
(人),
偶尔或不用网络外卖的有![]() (人).
(人).
则选出的3人中至少有2人经常使用网络外卖的概率为![]() .
.
②由![]() 列联表,可知抽到经常使用网络外卖的网民的频率为
列联表,可知抽到经常使用网络外卖的网民的频率为![]() ,
,
将频率视为概率,即从![]() 市市民中任意抽取1人,
市市民中任意抽取1人,
恰好抽到经常使用网络外卖的市民的概率为![]() .
.
由题意得![]() ,
,
所以![]() ;
;
![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 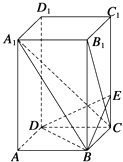
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1 , S3 , 3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an , cn= ![]() ,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围.
,记数列{cn}的前n项和为Tn . 若对于任意的n∈N* , Tn≤λ(n+4)恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y= ![]() x3+bx2+(b+2)x+3是R上的单调增函数,则b的取值是( )
x3+bx2+(b+2)x+3是R上的单调增函数,则b的取值是( )
A.b<﹣1或b>2
B.b≤﹣2或b≥2
C.﹣1<b<2
D.﹣1≤b≤2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在求函数y=lgx和 ![]() 的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )
x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
A.(2.125,2,25)
B.(2.75,2.875)
C.(2.625,2.75)
D.(2.5,2.625)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com