
【题目】已知椭圆![]() 的长轴为
的长轴为![]() ,且过点
,且过点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 为原点,若点
为原点,若点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,试判断直线
,试判断直线![]() 与圆
与圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
【答案】(1)![]() (2)直线
(2)直线![]() 与圆
与圆![]() 相切,证明见解析
相切,证明见解析
【解析】
(1)由题意可得![]() ,代入
,代入![]() 的坐标,可得
的坐标,可得![]() ,
,![]() 的方程,解方程可得椭圆方程;
的方程,解方程可得椭圆方程;
(2)设出点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,其中
,其中![]() ,由
,由![]() 得到
得到![]() ,用坐标表示后把
,用坐标表示后把![]() 用含有
用含有![]() 点的坐标表示,然后分
点的坐标表示,然后分![]() ,
,![]() 的横坐标相等和不相等写出直线
的横坐标相等和不相等写出直线![]() 的方程,然后由圆
的方程,然后由圆![]() 的圆心到
的圆心到![]() 的距离和圆的半径相等,证明直线
的距离和圆的半径相等,证明直线![]() 与圆
与圆![]() 相切.
相切.
(1)由题意可得![]() ,即
,即![]() ,
,
又![]() ,解得
,解得![]() ,
,
即有椭圆![]() 的方程为
的方程为![]() ;
;
(2)直线![]() 与圆
与圆![]() 相切.
相切.
证明如下:设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,其中
,其中![]() .
.
![]() ,
,
![]() ,即
,即![]() ,
,
解得![]() .
.
当![]() 时,
时,![]() ,代入椭圆
,代入椭圆![]() 的方程,得
的方程,得![]() ,
,
故直线![]() 的方程为
的方程为![]() ,
,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() .
.
此时直线![]() 与圆
与圆![]() 相切.
相切.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
即![]() .
.
圆心![]() 到直线
到直线![]() 的距离
的距离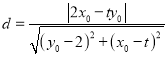
又![]() ,
,![]() .
.
故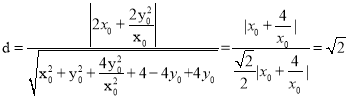 .
.
此时直线![]() 与圆
与圆![]() 相切.
相切.
综合得直线![]() 与圆
与圆![]() 相切.
相切.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 对其定义域内的任意
对其定义域内的任意![]() ,
,![]() ,当
,当![]() 时总有
时总有![]() ,则称
,则称![]() 为紧密函数,例如函数
为紧密函数,例如函数![]() 是紧密函数,下列命题:
是紧密函数,下列命题:
![]() 紧密函数必是单调函数;
紧密函数必是单调函数;![]() 函数
函数![]() 在
在![]() 时是紧密函数;
时是紧密函数;
![]() 函数
函数![]() 是紧密函数;
是紧密函数;
![]() 若函数
若函数![]() 为定义域内的紧密函数,
为定义域内的紧密函数,![]() ,则
,则![]() ;
;
![]() 若函数
若函数![]() 是紧密函数且在定义域内存在导数,则其导函数
是紧密函数且在定义域内存在导数,则其导函数![]() 在定义域内的值一定不为零.
在定义域内的值一定不为零.
其中的真命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面为正方形,△PAD为等边三角形,平面PAD丄平面PCD.
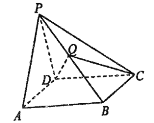
(1)证明:平面PAD丄平面ABCD:
(2)若AB=2,Q为线段的中点,求三棱锥Q-PCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区初中学生的体质健康情况,统计了该地区8所学校学生的体质健康数据,按总分评定等级为优秀,良好,及格,不及格.良好及其以上的比例之和超过40%的学校为先进校.各等级学生人数占该校学生总人数的比例如下表:
比例 学校 等级 | 学校A | 学校B | 学校C | 学校D | 学校E | 学校F | 学校G | 学校H |
优秀 | 8% | 3% | 2% | 9% | 1% | 22% | 2% | 3% |
良好 | 37% | 50% | 23% | 30% | 45% | 46% | 37% | 35% |
及格 | 22% | 30% | 33% | 26% | 22% | 17% | 23% | 38% |
不及格 | 33% | 17% | 42% | 35% | 32% | 15% | 38% | 24% |
(1)从8所学校中随机选出一所学校,求该校为先进校的概率;
(2)从8所学校中随机选出两所学校,记这两所学校中不及格比例低于30%的学校个数为X,求X的分布列;
(3)设8所学校优秀比例的方差为S12,良好及其以下比例之和的方差为S22,比较S12与S22的大小.(只写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六棱锥P﹣ABCDEF中,六边形ABCDEF为正六边形,平面PAB⊥平面ABCDEF,AB=1,PA![]() ,PB=2.
,PB=2.
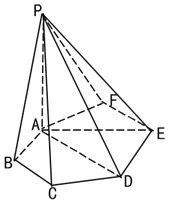
(1)求证:PA⊥平面ABCDEF;
(2)求直线PD与平面PAE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,E,F分别为
,E,F分别为![]() ,
,![]() 的中点.
的中点.
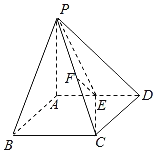
(1)求证:![]() 平面
平面![]() ;
;
(2)点G是线段![]() 上一动点,若
上一动点,若![]() 与平面
与平面![]() 所成最大角的正切值为
所成最大角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了学生的健康,对课间操活动做了如下规定:课间操时间若有雾霾则停止课间操,若无雾霾则组织课间操.预报得知,在未来一周从周一到周五的课间操时间出现雾霾的概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,且每一天出现雾霾与否是相互独立的.
,且每一天出现雾霾与否是相互独立的.
(1)求未来5天至少一天停止课间操的概率;
(2)求未来5天组织课间操的天数X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com