【题目】已知椭圆
的离心率为
，左顶点为
，过原点且斜率不为0的直线与椭圆交于
两点，其中点
在第二象限，过点
作
轴的垂线交
于点
．
⑴求椭圆的标准方程；
⑵当直线
的斜率为
时，求
的面积；
⑶试比较
与
大小．
【答案】⑴
⑵
⑶见解析
【解析】试题分析：（1）利用离心率、左顶点坐标求解即可；（2）根据直线过原点且斜率为
写出直线方程，联立直线和椭圆方程，求出
，再写出直线
的方程，求出点
的坐标，利用三角形的面积公式进行求解；（3）设直线
的方程为
， 
，与椭圆方程联立，得到关于
的一元二次方程，利用根与系数的关系、弦长公式及椭圆的对称性进行求解.
试题解析：⑴因为左顶点为
，所以
因为椭圆的离心率为
，所以
，解得
又因为
，所以
故所求椭圆的标准方程为
⑵因为直线
过原点，且斜率为
所以直线
的方程为
代入椭圆方程
解得
因为
，所以直线
的方程为
从而有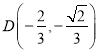
故
的面积等于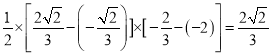
⑶方法一：
设直线
的方程为
， 
代入椭圆方程得
设
，则有
，解得
从而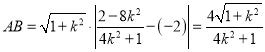
由椭圆对称性可得
所以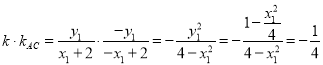
于是
故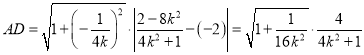
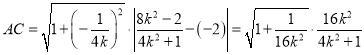
从而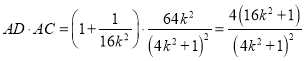
所以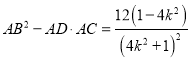
因为点
在第二象限，所以
，于是有
方法二：
设点
，则点
因为
，所以直线
的方程为
所以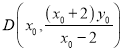
从而
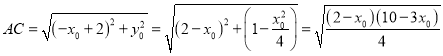
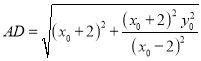
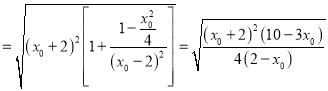
从而有
天天练口算系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，若椭圆
与圆
相交于
两点，且圆
在椭圆
内的弧长为
．
（1）求
的值；
（2）过椭圆
的中心作两条直线
交椭圆
于
和
四点，设直线
的斜率为
， 
的斜率为
，且
．
①求直线
的斜率；
②求四边形
面积的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图,曲线
由曲线
和曲线
组成,其中点
为曲线
所在圆锥曲线的焦点,点
为曲线
所在圆锥曲线的焦点,
(1)若
,求曲线
的方程;
(2)如图,作直线
平行于曲线
的渐近线,交曲线
于点
,
求证:弦
的中点
必在曲线
的另一条渐近线上;
(3)对于(1)中的曲线
,若直线
过点
交曲线
于点
,求△
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f(x)=Asin(ωx+φ)
的部分图象如图所示.
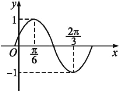
(1)求f(x)的最小正周期及解析式;
(2)设函数g(x)=f(x)-cos 2x,求g(x)在区间
上的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某射击运动员射击1次，命中10环、9环、8环、7环（假设命中的环数都为整数）的概率分别为0.20，0.22，0.25，0.28. 计算该运动员在1次射击中：
(1)至少命中7环的概率；
(2)命中不足8环的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=cosx（
sinx-cosx）+m（m∈R），将y=f（x）的图象向左平移
个单位后得到g（x）的图象，且y=g（x）在区间[
]内的最小值为
．
（1）求m的值；
（2）在锐角△ABC中，若g（
）=
，求sinA+cosB的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】成等差数列的三个正数的和等于15，并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）数列{bn}的前n项和为Sn，求证：数列{Sn+
}是等比数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，已知直线l：x-y-2=0，抛物线C：y2=2px(p＞0).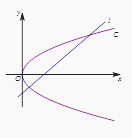
（1）若直线l过抛物线C的焦点，求抛物线C的方程；
（2）已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证：线段PQ的中点坐标为（2-p ， -p）；
②求p的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）=xlnx﹣ax2+（2a﹣1）x，a∈R．
（1）令g（x）=f′（x），求g（x）的单调区间；
（2）已知f（x）在x=1处取得极大值，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com