
����Ŀ��ij��˾�з���һ���²�Ʒ����������ǰ��ͬʱ�ڼס�������������30������г�����.���������֣��׳��е���������![]() ������
������![]() �Ķ�Ӧ��ϵ����ͼ����ʾ�ĺ�����ϵ���ҳ��е���������
�Ķ�Ӧ��ϵ����ͼ����ʾ�ĺ�����ϵ���ҳ��е���������![]() ������
������![]() �Ķ�Ӧ��ϵ����ͼ����ʾ�ĺ�����ϵ��ÿ����Ʒ����������
�Ķ�Ӧ��ϵ����ͼ����ʾ�ĺ�����ϵ��ÿ����Ʒ����������![]() ������
������![]() �Ķ�Ӧ��ϵ����ͼ����ʾ�ĺ�����ϵ��ͼ���������ߵ�һ����.
�Ķ�Ӧ��ϵ����ͼ����ʾ�ĺ�����ϵ��ͼ���������ߵ�һ����.
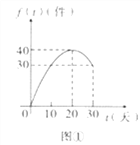
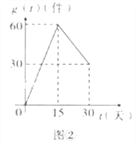

��������ò�Ʒ������ʱ��Ϊ![]() ��������������Ϊ
��������������Ϊ![]() ����
����![]() �Ľ���ʽ��
�Ľ���ʽ��
����������![]() �������У�����������������һ�쳬��
�������У�����������������һ�쳬��![]() ��Ԫ�������Ͷ�������������ò�Ʒ�Ƿ����Ͷ��������������˵������.
��Ԫ�������Ͷ�������������ò�Ʒ�Ƿ����Ͷ��������������˵������.
���𰸡�(1) 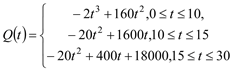 ,(2) ��һ���µ������У�û��һ�������������2��Ԫ��������Ͷ����������..
,(2) ��һ���µ������У�û��һ�������������2��Ԫ��������Ͷ����������..
�����������������������������������ۣ���![]() ʱ����
ʱ����![]() ʱ����
ʱ����![]() ʱ���ֱ����������������ĺ���ÿ����������Ļ��ɵý�����������ֱ�������κ��������ֵ������ÿ�κ��������ֵ��������
ʱ���ֱ����������������ĺ���ÿ����������Ļ��ɵý�����������ֱ�������κ��������ֵ������ÿ�κ��������ֵ��������![]() �����Բ�����Ͷ����������.
�����Բ�����Ͷ����������.
�����������1��![]() ��
��![]() ��
��
![]()
![]()
�����֪��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() .
.
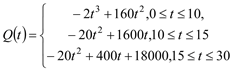 ��
��![]() ��
��
���ò�Ʒ������Ͷ�������������������£�
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() �����ֵΪ
�����ֵΪ![]() ��
��
��![]() ��
��
����һ���µ������У�û��һ�������������2��Ԫ��������Ͷ����������.


 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У������� ![]() ��б��Ϊk��ֱ��l����Բ
��б��Ϊk��ֱ��l����Բ ![]() ��������ͬ�Ľ���P��Q��
��������ͬ�Ľ���P��Q��
������k��ȡֵ��Χ��
��������Բ��x�������ᡢy��������Ľ���ֱ�ΪA��B���Ƿ���ڳ���k��ʹ������ ![]() ��
�� ![]() ���ߣ�������ڣ���kֵ����������ڣ���˵�����ɣ�
���ߣ�������ڣ���kֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A={x| ![]() ��3x��9}��B={x|log2x��0}��
��3x��9}��B={x|log2x��0}��
��1����A��B��A��B��
��2������A��B={x|x��A��xB}����A��B��B��A��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ֱ�����Բ
�ֱ�����Բ![]() �����ҽ��㣬����
�����ҽ��㣬����![]() ��
��![]() �ϣ�����
�ϣ�����![]() ���ӳ�
���ӳ�![]() ��
��![]() �㣬ʹ��
�㣬ʹ��![]() �����
�����![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() .
.
(1)��![]() �ķ��̣�
�ķ��̣�
(2)��![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ������
������![]() ��
��![]() ��
��![]() �㣬��ֱ��
�㣬��ֱ��![]() ��б����ֱ��
��б����ֱ��![]() ��б�ʴ����Ҳ�Ϊ�㣬֤��: ������ֱ�ߵ�б��֮��Ϊ��ֵ.
��б�ʴ����Ҳ�Ϊ�㣬֤��: ������ֱ�ߵ�б��֮��Ϊ��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4�D4������ϵ���������]
��ֱ������ϵxOy�У�����C�IJ�������Ϊ![]() ����Ϊ��������ֱ��l�IJ�������Ϊ
����Ϊ��������ֱ��l�IJ�������Ϊ![]() .
.
��1����a=1����C��l�Ľ������ꣻ
��2����C�ϵĵ㵽l�ľ�������ֵΪ![]() ����a.
����a.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��x3��x��2�ڵ�P0��������l1ƽ����ֱ��4x��y��1��0���ҵ�P0�ڵ������ޣ�
(1)��P0�����ꣻ(2)��ֱ��l��l1����lҲ���е�P0����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ʵ��
��ʵ��![]() ����
����![]() ��
��![]() ��������
��������![]() ��ʵ��
��ʵ��![]() ����
����![]() .
.
��1����![]() �ҡ�
�ҡ�![]() ��Ϊ�棬��ʵ��
��Ϊ�棬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ��
��![]() �ij�ֲ���Ҫ��������ʵ��
�ij�ֲ���Ҫ��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���![]() ������˵���������
������˵���������
A. ![]() ��
��![]() ����Сֵ��
����Сֵ��
B. ����![]() ����ֻ��1�����
����ֻ��1�����
C. ������ʵ��![]() ��ʹ��
��ʹ��![]() �����
�����
D. ��������������ȵ���ʵ��![]() ����
����![]() ����
����![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com