
 已知函数f(x)=
已知函数f(x)=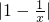 ,x∈(0,+∞).
,x∈(0,+∞).
 ,
, ,由
,由
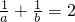 ,
,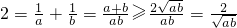 ,∴
,∴ ,即ab≥1
,即ab≥1 ,
,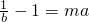 ,得a=b,舍去.
,得a=b,舍去. ,
, ,∴a,b是方程mx2-x+1=0的两个不相等实根,且这
,∴a,b是方程mx2-x+1=0的两个不相等实根,且这 ,解得
,解得
 (x∈(0,+∞))的图象先做一次关于x轴的对称变换,再向上平移一个单位,再做一次纵向的对折变换得到,由此可得函数y=f(x)的大致图象,进而根据图象下降对应函数的单调递减区间,图象上升对应函数的单调递增区间得到答案
(x∈(0,+∞))的图象先做一次关于x轴的对称变换,再向上平移一个单位,再做一次纵向的对折变换得到,由此可得函数y=f(x)的大致图象,进而根据图象下降对应函数的单调递减区间,图象上升对应函数的单调递增区间得到答案

 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com