
【题目】经市场调查,某旅游城市在过去的一个月内(以30天计),第t天(1≤t≤30,t∈N*)的旅游人数f(t)(单位:万人)近似地满足f(t)=4+ ![]() ,而人均日消费俄g(t)(单位:元)近似地满足g(t)=
,而人均日消费俄g(t)(单位:元)近似地满足g(t)= ![]() .
.
(1)试求所有游客在该城市旅游的日消费总额W(t)(单位:万元)与时间t(1≤t≤30,t∈N*)的函数表达式;
(2)求所有游客在该城市旅游的日消费总额的最小值.
【答案】
(1)解:由题意,根据该城市的旅游日消费总额=日旅游人数×人均消费的钱数,
可得:W(t)=f(t)g(t)
= 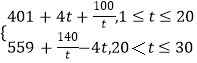 ;
;
(2)解:由(1)可知:当t∈[1,20]时,401+4t+ ![]() ≥401+2
≥401+2 ![]() =441,
=441,
当且仅当4t= ![]() 即t=5时取等号;
即t=5时取等号;
当t∈(20,30]时,因为W(t)=559+ ![]() ﹣4t递减,
﹣4t递减,
所以t=30时,W(t)有最小值W(30)=443+ ![]() ,
,
∵443+ ![]() >441,
>441,
∴t∈[1,30]时,W(t)的最小值为441万元.
【解析】(1)利用日消费总额=日旅游人数×人均消费的钱数,化简即得结论;(2)通过(1)可知当t∈[1,20]时利用基本不等式可知当且仅当t=5时取最小值441,当t∈(20,30]时利用函数的单调性可知当t=30时W(t)有最小值443+ ![]() ,进而比较即得结论.
,进而比较即得结论.


科目:高中数学 来源: 题型:
【题目】某个体户计划经销A,B两种商品,据调查统计,当投资额为x(x≥0)万元时,在经销A,B商品中所获得的收益分别为f(x)万元与g(x)万元,其中f(x)=a(x-1)+2,g(x)=6ln(x+b)(a>0,b>0).已知投资额为零时收益为零.
(1)求a,b的值;
(2)如果该个体户准备投入5万元经销这两种商品,请你帮他制定一个资金投入方案,使他能获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是各项均为正数的等比数列,且a1=3,a2+a3=36.
(1)求数列{an}的通项公式;
(2)若数列{bn}对任意的正整数n都有 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =2n+1,求b1+b2+b3+…+b2015的值.
=2n+1,求b1+b2+b3+…+b2015的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为![]() (a>0).
(a>0).
(1)求直线l与曲线C1的交点的极坐标(ρ,θ)(ρ≥0,0≤θ<2π);
(2)若直线l与C2相切,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3-3(a+1)x2+6ax+8,其中a∈R.
(1)若f(x)在x=3处取得极值,求常数a的值;
(2)若f(x)在(-∞,0)上为增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2-5ax+4a2<0,其中a>0,q:3<x≤4.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为![]() ,则直线BE与平面ACD所成角的正弦值为( )
,则直线BE与平面ACD所成角的正弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(t为参数),在以坐标原点O为极点,x轴的正非负半轴为极轴,取相同单位长度的极坐标系中,圆的极坐标方程为ρ=4sinθ.
(1)求直线l被圆截得的弦长;
(2)从极点作圆C的弦,求各弦中点的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com