
【题目】已知函数![]() ,
,![]() 为常数,且
为常数,且![]() .
.
(1)证明函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
(2)当![]() 时,讨论方程
时,讨论方程![]() 解的个数;
解的个数;
(3)若![]() 满足
满足![]() ,但
,但![]() ,则称
,则称![]() 为函数
为函数![]() 的二阶周期点,则
的二阶周期点,则![]() 是否有两个二阶周期点,说明理由.
是否有两个二阶周期点,说明理由.
【答案】(1)略;(2)当![]() 或
或![]() 时,方程有2个解;当
时,方程有2个解;当![]() 时,方程有3个解;当
时,方程有3个解;当![]() 时,方程有4个解;(3)只有
时,方程有4个解;(3)只有![]() 是二阶周期点.
是二阶周期点.
【解析】
(1)根据函数对称的性质即可证明函数![]() 的图像关于直线
的图像关于直线![]() 对称。
对称。
(2)当![]() 时,求出
时,求出![]() 的表达式,利用数形结合得到结论。
的表达式,利用数形结合得到结论。
(3)根据阶周期点的定义,分别求满足条件的![]() ,即可得到结论。
,即可得到结论。
(1)证明:设点![]() 为
为![]() 上任意一点,则
上任意一点,则
![]()
![]()
![]()
![]()
所以,函数![]() 的图像关于直线
的图像关于直线![]() 对称。
对称。
(2)当![]() 时
时
 ,
,
所以,当![]() 时,方程有
时,方程有![]() 个解;
个解;![]() 时,方程有
时,方程有![]() 个解;当
个解;当![]() 时,方程有
时,方程有![]() 个解;当
个解;当![]() 时,方程有
时,方程有![]() 个解。
个解。
综上:当![]() 或
或![]() 时,方程有
时,方程有![]() 个解;当
个解;当![]() 时,方程有
时,方程有![]() 个解;当
个解;当![]() 时,方程有
时,方程有![]() 个解。
个解。
(3)因为![]() ,
,
所以当![]() ,
,
若![]() ,即
,即![]() ,
,
若![]() ,即
,即![]() ,
,
当![]() ,同理可得:
,同理可得:
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
所以 ,
,
从而由![]() 得
得![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
所以只有![]() 是二阶周期点。
是二阶周期点。


科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
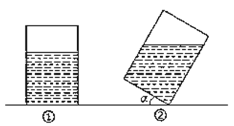
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 时曲线
时曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() ,
,![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() .在以坐标原点为极点,
.在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出圆![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点Q在
上,点Q在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E为AD的中点,AC与BE相交于点O.
,E为AD的中点,AC与BE相交于点O.

(1)证明:![]() 平面ABCD.
平面ABCD.
(2)求直线BC与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,数列
,数列![]() 是公比不为
是公比不为![]() 的等比数列.
的等比数列.
(1)求实数![]() 的值;
的值;
(2)设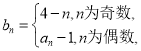 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 恰好为数列
恰好为数列![]() 中的项.
中的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:直线关于圆的圆心距单位![]() 圆心到直线的距离与圆的半径之比.
圆心到直线的距离与圆的半径之比.
(1)设圆![]() ,求过点
,求过点![]() 的直线关于圆
的直线关于圆![]() 的圆心距单位
的圆心距单位![]() 的直线方程.
的直线方程.
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且直线
,且直线![]() 关于圆
关于圆![]() 的圆心距单位
的圆心距单位![]() ,求此圆
,求此圆![]() 的方程.
的方程.
(3)是否存在点![]() ,使过点
,使过点![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 与
与![]() 的圆心距单位始终相等?若存在,求出相应的
的圆心距单位始终相等?若存在,求出相应的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com