
【题目】下列有关命题的说法正确的是( )
A. “若x>1,则2x>1”的否命题为真命题
B. “若cosβ=1,则sinβ=0”的逆命题是真命题
C. “若平面向量a,b共线,则a,b方向相同”的逆否命题为假命题
D. 命题“若x>1,则x>a”的逆命题为真命题,则a>0
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表,
,部分对应值如下表,![]() 的导函数
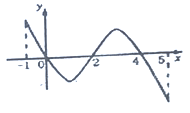
的导函数![]() 的图象如图所示,给出关于
的图象如图所示,给出关于![]() 的下列命题:
的下列命题:
①函数![]() 在
在![]() 处取得极小值;
处取得极小值;
②函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 是增函数;
是增函数;
③当![]() 时,函数
时,函数![]() 有4个零点;
有4个零点;
④如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值为0.
的最小值为0.
其中所有的正确命题是__________(写出正确命题的序号).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机将1,2,…,2n(n∈N* , n≥2)这2n个连续正整数分成A、B两组,每组n个数,A组最小数为a1 , 最大数为a2;B组最小数为b1 , 最大数为b2;记ξ=a2﹣a1 , η=b2﹣b1 .
(1)当n=3时,求ξ的分布列和数学期望;
(2)C表示事件“ξ与η的取值恰好相等”,求事件C发生的概率P(C);
(3)对(2)中的事件C, ![]() 表示C的对立事件,判断P(C)和P(
表示C的对立事件,判断P(C)和P( ![]() )的大小关系,并说明理由.
)的大小关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x+θ)+acos(x+2θ),其中a∈R,θ∈(﹣ ![]() ,
, ![]() )
)
(1)当a= ![]() ,θ=
,θ= ![]() 时,求f(x)在区间[0,π]上的最大值与最小值;
时,求f(x)在区间[0,π]上的最大值与最小值;
(2)若f( ![]() )=0,f(π)=1,求a,θ的值.
)=0,f(π)=1,求a,θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,且2a5-a3=13,S4=16.
(1)求数列{an}的前n项和Sn;
(2)设Tn=![]() (-1)iai,若对一切正整数n,不等式 λTn<[an+1+(-1)n+1an]·2n-1 恒成立,求实数 λ 的取值范围;
(-1)iai,若对一切正整数n,不等式 λTn<[an+1+(-1)n+1an]·2n-1 恒成立,求实数 λ 的取值范围;
(3)是否存在正整数m,n(n>m>2),使得S2,Sm-S2,Sn-Sm成等比数列?若存在,求出所有的m,n;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线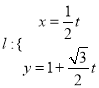 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com