
分析 (Ⅰ)由平面向量数量积的运算及三角函数中的恒等变换应用可得f(x)=2in(2x+$\frac{π}{6}$),根据正弦函数的单调性即可求得函数f(x)在区间[0,$\frac{π}{2}$]上的最大值和最小值;
(Ⅱ)由已知可得sin(A+$\frac{π}{6}$)=$\frac{3}{5}$,结合A的范围,可求cos(A+$\frac{π}{6}$)=-$\frac{4}{5}$,从而可求cosA=cos(A+$\frac{π}{6}$-$\frac{π}{6}$)的值,利用二倍角的余弦函数公式即可得解.
解答 解:(Ⅰ)∵f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=4sinxcos(x+$\frac{π}{6}$)+1
=4sinx($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)+1
=$\sqrt{3}$(2sinxcosx)+(1-2sin2x)
=$\sqrt{3}$sin2x+cos2x
=2in(2x+$\frac{π}{6}$),
∵f(x)=2in(2x+$\frac{π}{6}$)在区间[0,$\frac{π}{6}$]上为增函数,在区间[$\frac{π}{6}$,$\frac{π}{2}$]上为减函数,
又∵f(0)=1,f($\frac{π}{6}$)=2,f($\frac{π}{2}$)=-1,
∴函数f(x)在区间[0,$\frac{π}{2}$]上的最大值为2,最小值为-1.…7分
(Ⅱ)∵f($\frac{A}{2}$)=$\frac{6}{5}$,
∴sin(A+$\frac{π}{6}$)=$\frac{3}{5}$,
又∵$\frac{π}{3}<A<\frac{5π}{6}$,
∴$\frac{π}{2}$<A+$\frac{π}{6}$<π,
∴cos(A+$\frac{π}{6}$)=-$\frac{4}{5}$,
∴cosA=cos(A+$\frac{π}{6}$-$\frac{π}{6}$)=cos(A+$\frac{π}{6}$)cos$\frac{π}{6}$+sin(A+$\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{3-4\sqrt{3}}{10}$,
∴cos2A=2cos2A-1
=2$•\frac{57-24\sqrt{3}}{100}$-1
=$\frac{7-24\sqrt{3}}{50}$.…13分
点评 本题主要考查了平面向量数量积的运算,三角函数中的恒等变换应用,正弦函数的单调性,二倍角的余弦函数公式的应用,属于基本知识的考查.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
 某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.
某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| A. | 99% | B. | 95% | C. | 90% | D. | 无关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为π的偶函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为$\frac{π}{2}$的偶函数 | D. | 周期为π的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
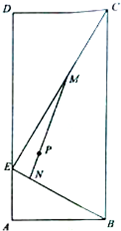 某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,
某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com