
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则称
,p为常数),则称![]() 为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
A.![]() 不是等方差数列;
不是等方差数列;
B.若![]() 既是等方差数列,又是等差数列,则该数列为常数列;
既是等方差数列,又是等差数列,则该数列为常数列;
C.已知数列![]() 是等方差数列,则数列
是等方差数列,则数列![]() 是等方差数列;
是等方差数列;
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列.
,k为常数)也是等方差数列.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面ABCD,侧棱
底面ABCD,侧棱![]() ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中![]() ,
,![]() ,
,![]() ,O为AD中点.
,O为AD中点.

(1)求异面直线PB与CD所成角的余弦值;
(2)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点,问在直线
两点,问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出点
恒成立?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意
,对于定义域内的任意![]() 存在实数
存在实数![]() 使得
使得![]() 成立,则称此函数具有“
成立,则称此函数具有“![]() 性质”.
性质”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,写出所有
性质”,写出所有![]() 的值;若不具有“
的值;若不具有“![]() 性质”,请说明理由.
性质”,请说明理由.
(2)设函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求当
,求当![]() 时函数
时函数![]() 的解析式;若
的解析式;若![]() 与
与![]()
![]() 交点个数为1001个,求
交点个数为1001个,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCPE中,平面PAC⊥平面ABC,AC⊥BC,PE∥BC,2PE=BC,M是线段AE的中点,N是线段PA上一点,且满足AN=![]() AP(0<
AP(0<![]() <1).
<1).
(Ⅰ)若![]() ,求证:MN⊥PC;
,求证:MN⊥PC;
(Ⅱ)是否存在![]() ,使得三棱锥M-ACN与三棱锥B-ACP的体积比为1:12?若存在,求出
,使得三棱锥M-ACN与三棱锥B-ACP的体积比为1:12?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某手机品牌公司的年固定成本为40万元,每生产1万部手机还需要另投入16万元,设该公句一年内生产x万部并全部销售完,每1万部手机的销售收入为![]() 万元,且
万元,且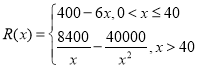 .
.
(1)写出年利润(万元)关于年产量![]() (万部)的函数解析式;
(万部)的函数解析式;
(2)当年产量多少万部时,公司在该款手机生产获得最大利润,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆O:![]() 与坐标轴分别交于A1,A2,B1,B2(如图).
与坐标轴分别交于A1,A2,B1,B2(如图).
(1)点Q是圆O上除A1,A2外的任意点(如图1),直线A1Q,A2Q与直线![]() 交于不同的两点M,N,求线段MN长的最小值;
交于不同的两点M,N,求线段MN长的最小值;
(2)点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设A2P的斜率为k,EF的斜率为m,求证:2m﹣k为定值.
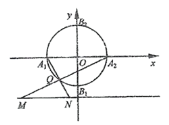
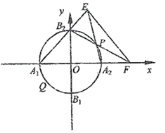
(图1) (图2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com