
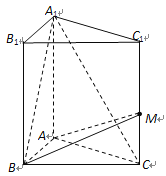
【题目】直三棱柱![]() 中,底面
中,底面![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 上一点,设
上一点,设![]() .
.
(1) 若![]() ,求
,求![]() 的值;
的值;
(2) 若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知在平面直角坐标系xOy中,O为坐标原点,曲线C: 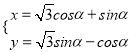 (α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ
(α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)曲线C上恰好存在三个不同的点到直线l的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中央广播电视总台2019主持人大赛》是中央人民广播电视总台成立后推出的第一个电视大赛,由撒贝宁担任主持人,康辉、董卿担任点评嘉宾,敬一丹、鲁健、朱迅、俞虹、李宏岩等![]() 位担任专业评审.从2019年10月26日起,每周六
位担任专业评审.从2019年10月26日起,每周六![]() 在中央电视台综合频道播出,某传媒大学为了解大学生对主持人大赛的关注情况,分别在大一和大二两个年级各随机抽取了
在中央电视台综合频道播出,某传媒大学为了解大学生对主持人大赛的关注情况,分别在大一和大二两个年级各随机抽取了![]() 名大学生进行调查.下图是根据调查结果绘制的学生场均关注比赛的时间频率分布直方图和频数分布表,并将场均关注比赛的时间不低于
名大学生进行调查.下图是根据调查结果绘制的学生场均关注比赛的时间频率分布直方图和频数分布表,并将场均关注比赛的时间不低于![]() 分钟的学生称为“赛迷”.
分钟的学生称为“赛迷”.
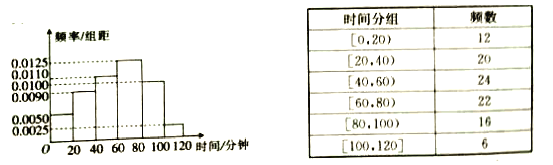
大一学生场均关注比赛时间的频率分布直方图大二学生场均关注比赛时间的频数分布表
(1)将频率视为概率,估计哪个年级的大学生是“赛迷”的概率大,请说明理由;
(2)已知抽到的![]() 名大一学生中有男生
名大一学生中有男生![]() 名,其中
名,其中![]() 名为“赛迷”.试完成下面的
名为“赛迷”.试完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为“赛迷”与性别有关.
的把握认为“赛迷”与性别有关.
非“赛迷” | “赛迷” | 合计 | |
男 | |||
女 | |||
合计 |
附: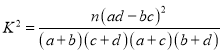 ,其中
,其中![]() span>.
span>.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com