
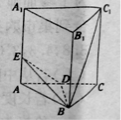
【题目】已知正三棱柱![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
(Ⅰ)当![]() 时,求证
时,求证![]() ;
;
(Ⅱ)是否存在点![]() ,使二面角
,使二面角![]() 等于60°?若存在,求
等于60°?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)存在点![]() ,当
,当![]() 时,二面角
时,二面角![]() 等于
等于![]() .
.
【解析】
试题分析:(Ⅰ)证明:连接![]() ,
,![]() 由
由![]() 为正三棱柱
为正三棱柱![]()
![]() 为正三角形
为正三角形![]()
![]() ,
,
又平面![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
![]()
![]() .易得
.易得![]()
![]()
![]() 丄平面
丄平面![]()
![]()
![]() .(Ⅱ)假设存在点
.(Ⅱ)假设存在点![]() 满足条件,设
满足条件,设![]() .由
.由![]() 丄平面
丄平面![]()
![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,求得平面
,求得平面![]() 的一个法向量为
的一个法向量为
![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]()
![]()
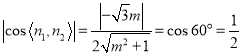
![]()
![]() .
.
试题解析:(Ⅰ)证明:连接![]() ,
,
因为![]() 为正三棱柱,所以
为正三棱柱,所以![]() 为正三角形,
为正三角形,
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,
,
所以![]() 丄平面
丄平面![]() ,
,![]() 面
面![]() ,所以
,所以![]() .
.
(Ⅱ)假设存在点![]() 满足条件,设
满足条件,设![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 丄平面
丄平面![]() ,
,
所以![]() ,
,
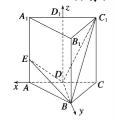
分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
则![]() ,
,
所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则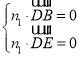 ,
,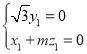 令
令![]() ,得
,得![]() ,
,
同理,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则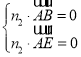 ,
,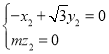 取
取![]() ,
,
∴![]() .
.
∴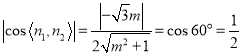 ,解得
,解得![]() ,
,
故存在点![]() ,当
,当![]() 时,二面角
时,二面角![]() 等于
等于![]() .
.


科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在 ![]() 人或
人或 ![]() 人以下,每人需交费用为
人以下,每人需交费用为 ![]() 元;若旅行团人数多于
元;若旅行团人数多于 ![]() 人,则给予优惠:每多
人,则给予优惠:每多 ![]() 人,人均费用减少
人,人均费用减少 ![]() 元,直到达到规定人数
元,直到达到规定人数 ![]() 人为止.旅行社需支付各种费用共计
人为止.旅行社需支付各种费用共计 ![]() 元.
元.
Ⅰ 写出每人需交费用 ![]() 关于人数
关于人数 ![]() 的函数;
的函数;
Ⅱ 旅行团人数为多少时,旅行社可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一次函数f(x)为增函数,且f(f(x))=4x+9,g(x)=mx+m+3(m∈R).
(1)当x∈[-1,2]时,若不等式g(x)>0恒成立,求m的取值范围;
(2)如果函数F(x)=f(x)g(x)为偶函数,求m的值;
(3)当函数f(x)和g(x)满足f(g(x))=g(f(x))时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加师大附中第30界田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(Ⅰ)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(Ⅱ)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根![]() 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com