
分析 (Ⅰ)由条件利用三角函数的恒等变换化简函数的解析式,再利用正弦函数的周期性以及它的图象的对称性求得函数f(x)的最小正周期及其对称轴.
(Ⅱ)由条件利用正弦函数的定义域和值域,求得a,b的值.
解答 解:(Ⅰ)函数f(x)=asin($\frac{x}{2}+\frac{π}{6}$)-acos$\frac{x}{2}$+b=asin$\frac{x}{2}$cos$\frac{π}{6}$+acos$\frac{x}{2}$sin$\frac{π}{6}$-acos$\frac{x}{2}$+b
=a($\frac{\sqrt{3}}{2}$sin$\frac{x}{2}$-$\frac{1}{2}$cos$\frac{x}{2}$)+b=asin($\frac{x}{2}$-$\frac{π}{6}$)+b,
故函数的最小正周期为 $\frac{2π}{\frac{1}{2}}$=4π.
令$\frac{x}{2}$-$\frac{π}{6}$=kπ+$\frac{4π}{3}$,k∈z,求得x=2kπ+$\frac{4π}{3}$,k∈z,可得函数的图象的对称轴为 x=2kπ+$\frac{4π}{3}$,k∈z.
(Ⅱ)∵x∈[-π,$\frac{2π}{3}$]上,∴$\frac{x}{2}$-$\frac{π}{6}$∈[-$\frac{2π}{3}$,$\frac{π}{6}$],∴-1≤sin($\frac{x}{2}$-$\frac{π}{6}$)≤$\frac{1}{2}$.
再结合题意以及a>0,可得 $\left\{\begin{array}{l}{-a+b=-1}\\{\frac{a}{2}+b=2}\end{array}\right.$,求得 $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$.
点评 本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,正弦函数的周期性以及它的图象的对称性,三角函数的周期性和求法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2016×2 017 | B. | 2015×2 016 | C. | 2014×2 015 | D. | 2016×2 016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| A. | 99% | B. | 95% | C. | 90% | D. | 无关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
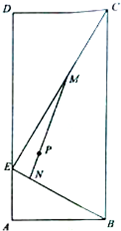 某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,
某生态农庄池塘的平面图为矩形ABCD,已知AB=4,BC=10,E为AD上一点,且AE=2,P为池塘内一临时停靠点,且P到AB,BC的距离均为3,EC,EB为池塘上浮桥,为了固定浮桥,现准备进过临时停靠点P再架设一座浮桥MN,其中M,N分别是浮桥EC,EB上点.(浮桥宽度、池塘岸边宽度不计),设EM=d,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
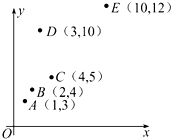 有一散点图如图所示,在5个(x,y)数据中去掉D(3,10)后,下列说法正确的是( )
有一散点图如图所示,在5个(x,y)数据中去掉D(3,10)后,下列说法正确的是( )| A. | 残差平方和变小 | |
| B. | 相关系数r变小 | |
| C. | 相关指数R2变小 | |
| D. | 解释变量x与预报变量y的相关性变弱 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com