
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() .
.
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 若存在![]() ,使不等式
,使不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)已知函数![]() 满足
满足![]() ,且规定
,且规定![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)6.
;(Ⅲ)6.
【解析】
(Ⅰ)![]() 定义在
定义在![]() 上的奇函数,所以利用特殊值
上的奇函数,所以利用特殊值![]() 求解
求解![]() ,然后检验即可. (Ⅱ)首先根据定义证明函数
,然后检验即可. (Ⅱ)首先根据定义证明函数![]() 在
在![]() 上单调递减,然后再根据单调性将
上单调递减,然后再根据单调性将![]() 等价转化为
等价转化为![]() 有解,即
有解,即![]() ,求二次函数的最小值,即可解出实数
,求二次函数的最小值,即可解出实数![]() 的取值范围. (Ⅲ)首先根据
的取值范围. (Ⅲ)首先根据![]() ,
,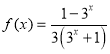 ,解出
,解出![]() ,代入
,代入![]() 得到解析式
得到解析式![]() ,令
,令![]() ,(
,(![]() ),则
),则![]() ,利用基本不等式求最值求出
,利用基本不等式求最值求出![]() .
.
(Ⅰ)![]() 是
是![]() 上的奇函数,
上的奇函数,![]() ,
,

![]() ,
,
当![]() 时,
时,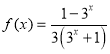 ,
,
此时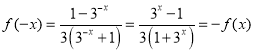
![]() 是奇函数成立.
是奇函数成立.
![]() ;
;
(Ⅱ)任取![]() 且
且![]() ,
,
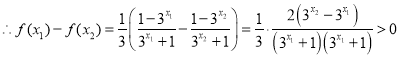 ,
,
![]()
![]() ,
,
![]()
![]() 上为减函数.
上为减函数.
若存在![]() ,使不等式
,使不等式![]() 有解,则
有解,则![]() 有解
有解
![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
(Ⅲ)![]() ,
,
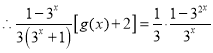 ,
,
![]() ,
,
![]() ,且
,且![]() 也适合,
也适合,
![]() ,
,
任意![]() ,不等式
,不等式![]() 恒成立,
恒成立,
![]() ,
,
令![]()
![]() ,
,
令![]() ,
,
任取![]() 且
且![]() ,
,
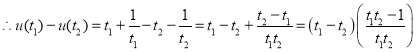 ,
,
当![]() 时,
时,![]() ,
,![]() 上为增函数.
上为增函数.
当![]() 时,
时,![]() ,
,![]() 上为减函数.
上为减函数.
![]() 时
时![]() 即
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,同理
,同理![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
![]() 时
时![]()
![]() ,
,![]() 的最大值为6.
的最大值为6. ![]()


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】 设函数![]()
(1)如果![]() ,那么实数
,那么实数![]() ___;
___;
(2)如果函数![]() 有且仅有两个零点,那么实数
有且仅有两个零点,那么实数![]() 的取值范围是___.
的取值范围是___.
【答案】![]() 或4;
或4;![]()
【解析】
试题分析:由题意![]() ,解得
,解得![]() 或
或![]() ;
;
第二问如图:
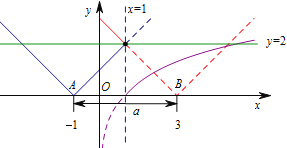
![]() 的图象是由两条以
的图象是由两条以![]() 为顶点的射线组成,当
为顶点的射线组成,当![]() 在A,B 之间(包括
在A,B 之间(包括![]() 不包括
不包括![]() )时,函数
)时,函数![]() 和
和![]() 有两个交点,即
有两个交点,即![]() 有两个零点.所以
有两个零点.所以![]() 的取值范围为
的取值范围为![]() .
.
考点:1.分段函数值;2.函数的零点.
【题型】填空题
【结束】
15
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
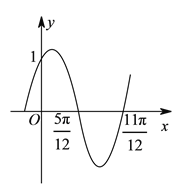
(![]() )求函数
)求函数![]() 的解析式.
的解析式.
(![]() )求函数
)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①如果![]() 、
、![]() 是两条直线,
是两条直线,![]() ,那么
,那么![]() 平行于过
平行于过![]() 的任何一个平面;②如果直线
的任何一个平面;②如果直线![]() 满足
满足![]() ,那么
,那么![]() 与平面
与平面![]() 内的任何一条直线平行;③如果直线
内的任何一条直线平行;③如果直线![]() 、
、![]() 满足
满足![]() ,
,![]() ,则
,则![]() ;④如果直线
;④如果直线![]() 、
、![]() 和平面
和平面![]() 满足
满足![]() ,
,![]() ,
,![]() ,那么
,那么![]() ;⑤如果
;⑤如果![]() 与平面
与平面![]() 内的无数条直线平行,那么直线
内的无数条直线平行,那么直线![]() 必平行于平面
必平行于平面![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足不等式|x![]() A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b
A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b![]() t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:

(1)根据表格提供的数据求出函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 的周期为
的周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由;
的范围(或值),若不存在,请说明理由;
(3)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 时,
时,![]() 的值为2千克/年;当
的值为2千克/年;当![]() 时,
时,![]() 是
是![]() 的一次函数;当
的一次函数;当![]() 时,因缺氧等原因,
时,因缺氧等原因,![]() 的值为0千克/年.
的值为0千克/年.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当养殖密度![]() 为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多少时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com