
����Ŀ��Ϊ��̽��ij�и����������ڸ߿�־Ը�б����������ࡱרҵ�Ƿ����Ա��йأ��ִӸ��и����������������ȡ50��ѧ�����е��飬�õ�����2��2������������λ���ˣ���
�����������ࡱ | �����������ࡱ | �ϼ� | |
�� | 6 | 24 | 30 |
Ů | 14 | 6 | 20 |
�ϼ� | 20 | 30 | 50 |
���ݴ��������ܷ���99%�İ�����Ϊ�����������������ࡱרҵ���Ա��йأ�
�������������и��¼���Ƶ����Ϊ���ʹ���ȫ�����忼���ı���������ִӸ��е�ȫ�忼���������ڶࣩ�������ȡ3�ˣ���3���б����������ࡱרҵ������Ϊ�������X�����������X�ĸ��ʷֲ�����ѧ������
�����ο����ݣ�
P��X2��k�� | 0.05 | 0.010 |
k | 3.841 | 6.635 |
���ο���ʽ��X2= ![]() ��
��
���𰸡��⣺���� ![]() ����99%�İ�����Ϊ������Ը�ⱨ���������ࡱרҵ���Ա��й�
����99%�İ�����Ϊ������Ը�ⱨ���������ࡱרҵ���Ա��й�
�����Ƹ��е�ȫ�忼������һ�˱����������ࡱרҵ�ĸ���Ϊ ![]()
X�Ŀ���ȡֵΪ0��1��2��3�������⣬��X��B��3�� ![]() ����
���� ![]()
���������X�ķֲ���Ϊ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
���������X����ѧ���� ![]()
����������I������K2 �� �����ٽ�ֵ���������ۣ���II���ֱ����X=0��1��2��3ʱ�ĸ��ʵó��ֲ��У����ݷֲ��еó���ѧ�����ͷ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ó��Ħ������.�ر����������ҹ���Ϊ������.���������Ի�Ϊ�����������ٰ���ѣ������ϼӴ�Ը�����ʩѹ����£���ǵ��ƻ�Ϊ5G��Ȼ���Ⲣû���û�Ϊȴ��.��Ϊ��2018�겻���������¼�¼����������ͬ��ǿ��.���꣬�ҹ���Ϊijһ��ҵΪ�˽�һ�������г����������ƻ���2020�������¼�������ij�����ֻ�.ͨ���г������������˿��ֻ�ȫ����Ͷ��̶��ɱ�250��ÿ����![]() ��ǧ�����ֻ�������Ͷ��ɱ�
��ǧ�����ֻ�������Ͷ��ɱ�![]() ��Ԫ����
��Ԫ����  �����г�����֪��ÿ���ֻ��ۼ�0.7��Ԫ����ȫ�����������ֻ�������ȫ��������.
�����г�����֪��ÿ���ֻ��ۼ�0.7��Ԫ����ȫ�����������ֻ�������ȫ��������.
��![]() �����2020�������
�����2020�������![]() ����Ԫ�����������
����Ԫ�����������![]() ��ǧ�����ĺ�����ϵʽ��������=���۶�ɱ�����
��ǧ�����ĺ�����ϵʽ��������=���۶�ɱ�����
![]() 2020�����Ϊ���٣�ǧ����ʱ����ҵ�������������������Ƕ��٣�
2020�����Ϊ���٣�ǧ����ʱ����ҵ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У�PA��ƽ��ABCD������ABCD��ֱ�����Σ�����AD��BC��AB��AD��AB=AD= ![]() BC��
BC�� ![]() =
= ![]()
![]() ��
�� 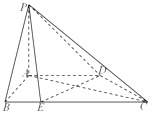
��1����֤��DE��ƽ��PAC��
��2����ֱ��PE��ƽ��PAC���ɽǵ�����ֵΪ ![]() ��������A��PC��D��ƽ��ǵ�����ֵ��
��������A��PC��D��ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C�� ![]() ��a��0��b��0�������ҽ���ֱ�ΪF1 �� F2 �� ��M��˫����C�Ľ��㲻�غϣ���M����F1 �� F2�ĶԳƵ�ֱ�ΪA��B���߶�MN���е���˫���ߵ���֧�ϣ���|AN|��|BN|=12����a=�� ��
��a��0��b��0�������ҽ���ֱ�ΪF1 �� F2 �� ��M��˫����C�Ľ��㲻�غϣ���M����F1 �� F2�ĶԳƵ�ֱ�ΪA��B���߶�MN���е���˫���ߵ���֧�ϣ���|AN|��|BN|=12����a=�� ��
A.3
B.4
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ����⣺
��Բ![]() ��ֱ��
��ֱ��![]() �ཻ�������ҳ�Ϊ
�ཻ�������ҳ�Ϊ![]() ��
��
��ֱ��![]() ��Բ
��Բ![]() ���й����㣻
���й����㣻
�����ⳤΪ![]() ��������Ķ��㶼��ͬһ�����ϣ������ı����Ϊ
��������Ķ��㶼��ͬһ�����ϣ������ı����Ϊ![]() ��
��
�����ⳤΪ![]() ����������Ķ��㶼��ͬһ�����ϣ����������Ϊ
����������Ķ��㶼��ͬһ�����ϣ����������Ϊ![]() .
.
���У���ȷ��������Ϊ__________����д��������ȷ�������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������½��ۣ�������ȷ���۵ĸ���Ϊ( )
�ٺ���![]() �����Ϊ
�����Ϊ![]() ������
������![]() ��ͼ����
��ͼ����![]() ʱ������ֵһ�����.
ʱ������ֵһ�����.
�������������֮������к���ֵ����ͬ��.
�ۺ���![]() ������
������![]() ��������������
��������������![]() ����
����![]() ������
������![]() ��һ����ʵ��.
��һ����ʵ��.
�ܡ����ַ������������ϵĺ�����������㶼��Ч.
A. 0��B. 1��C. 2��D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����5�����a1=0��a5=2����|ai+1��ai|=1��i=1��2��3��4�������������IJ�ͬ���еĸ���Ϊ��������
A.3
B.4
C.5
D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������a��R����
������a��R����
��1�����ۺ���f��x������ż�ԣ���˵�����ɣ�
��2����![]() �����жϺ���f��x��������[1��+�ޣ��ϵĵ����ԣ����ú��������Զ������֤����
�����жϺ���f��x��������[1��+�ޣ��ϵĵ����ԣ����ú��������Զ������֤����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com