
【题目】已知函数![]() 的部分图像如图所示.
的部分图像如图所示.
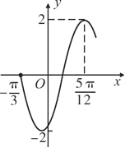
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调递减区间;
的单调递减区间;
(3)不画图,说明函数![]() 的图像经过怎样的变换可得到
的图像经过怎样的变换可得到![]() 的图像.
的图像.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 是过抛物线
是过抛物线![]() 的焦点F的一条弦,过点A(A在第一象限内)作直线
的焦点F的一条弦,过点A(A在第一象限内)作直线![]() 垂直于抛物线的准线,垂足为C,直线
垂直于抛物线的准线,垂足为C,直线![]() 与抛物线相切于点A,交x轴于点T,给出下列命题:
与抛物线相切于点A,交x轴于点T,给出下列命题:
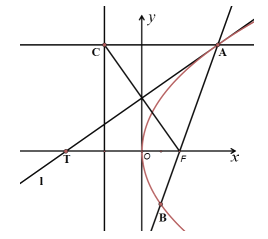
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正确的命题个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶100户贫困户.工作组对这100户村民的贫困状况和家庭成员受教育情况进行了调查:甲村55户贫困村民中,家庭成员接受过中等及以上教育的只有10户,乙村45户贫困村民中,家庭成员接受过中等及以上教育的有20户.
(1)完成下面的列联表,并判断是否有99.5%的把握认为贫困与接受教育情况有关;
家庭成员接受过中等以下 教育的户数 | 家庭成员接受过中等及以上 教育的户数 | 合计 | |
甲村贫困户数 | |||
乙村贫困户数 | |||
合计 |
(2)在被帮扶的100户贫困户中,按分层抽样的方法从家庭成员接受过中等及以上教育的贫困户中抽取6户,再从这6户中采用简单随机抽样的方法随机抽取2户,求这2户中甲、乙两村恰好各1户的概率.
参考公式与数据: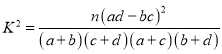 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x+2|,g(x)=|x+2|﹣|x﹣2a|+a.
(1)求不等式f(x)>4的解集;
(2)对x1∈R,x2∈R,使得f(x1)≥g(x2)成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com