
【题目】如下为简化的计划生育模型:每个家庭允许生男孩最多一个,即某一胎若为男孩,则不能再生下一胎,而女孩可以多个.为方便起见,此处约定每个家庭最多可生育3个小孩,即若第一胎或前两胎为女孩,则继续生,但若第三胎还是女孩,则不能再生了.设每一胎生男生女等可能,且各次生育相互独立.依据每个家庭最多生育一个男孩的政策以及我们对生育女孩的约定,令![]() 为某一家庭所生的女孩数,
为某一家庭所生的女孩数,![]() 为此家庭所生的男孩数.
为此家庭所生的男孩数.
(1)求![]() ,
,![]() 的分布列,并比较它们数学期望的大小;
的分布列,并比较它们数学期望的大小;
(2)求概率![]() ,其中
,其中![]() 为
为![]() 的方差.
的方差.
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
【题目】“今年我已经8个月没有戏拍了”迪丽热巴在8月的一档综艺节目上说,霍建华在家里开玩笑时说到“我失业很久了”;明道也在参加《演员请就位》时透露,已经大半年没有演过戏.为了了解演员的生存现状,什么样的演员才有戏演,有人搜集了内地、港澳台共计9481名演员的演艺生涯资料,在统计的所有演员资料后得到以下结论:①有![]() 的人在2019年没有在影剧里露过脸;②2019年备案的电视剧数量较2016年时下滑超过三分之一;③女演员面临的竞争更加激烈;④演员的艰难程度随着年龄的增加而降低.请问:以下判断正确的是( )
的人在2019年没有在影剧里露过脸;②2019年备案的电视剧数量较2016年时下滑超过三分之一;③女演员面临的竞争更加激烈;④演员的艰难程度随着年龄的增加而降低.请问:以下判断正确的是( )
A.调查采用了分层抽样B.调查采用了简单随机抽样
C.调查采用了系统抽样D.非抽样案例
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是菱形,PC⊥BC,点E是PC的中点,且平面PBC⊥平面ABCD.求证:
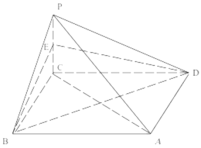
(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
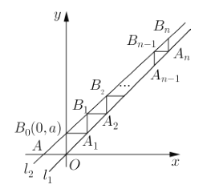
【题目】已知直线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与x轴交于点A,与y轴交于点
与x轴交于点A,与y轴交于点![]() ,过
,过![]() 作x 轴的平行线,交
作x 轴的平行线,交![]() 于点
于点![]() ,过
,过![]() 作y轴的平行线,交
作y轴的平行线,交![]() 于点
于点![]() ,再过
,再过![]() 作x轴的平行线交
作x轴的平行线交![]() 于点
于点![]() ,…,这样依次得线段
,…,这样依次得线段![]() 、
、![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、
、![]() ,记
,记![]() 为点
为点![]() 的横坐标,则
的横坐标,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() (其中
(其中![]() ,点P的轨迹记为曲线
,点P的轨迹记为曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线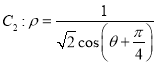 上.
上.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标
的公共点的极坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆C:
是椭圆C: ![]() 上一点,点P到椭圆C的两个焦点的距离之和为
上一点,点P到椭圆C的两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A,B是椭圆C上异于点P的两点,直线PA与直线![]() 交于点M,
交于点M,
是否存在点A,使得![]() ?若存在,求出点A的坐标;若不存在,请说明理由.
?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外卖平台为提高外卖配送效率,针对外卖配送业务提出了两种新的配送方案,为比较两种配送方案的效率,共选取50名外卖骑手,并将他们随机分成两组,每组25人,第一组骑手用甲配送方案,第二组骑手用乙配送方案.根据骑手在相同时间内完成配送订单的数量(单位:单)绘制了如下茎叶图:
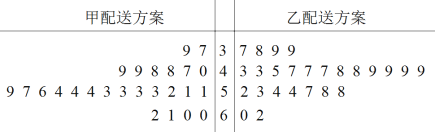
(1)根据茎叶图,求各组内25位骑手完成订单数的中位数,已知用甲配送方案的25位骑手完成订单数的平均数为52,结合中位数与平均数判断哪种配送方案的效率更高,并说明理由;
(2)设所有50名骑手在相同时间内完成订单数的平均数![]() ,将完成订单数超过
,将完成订单数超过![]() 记为“优秀”,不超过
记为“优秀”,不超过![]() 记为“一般”,然后将骑手的对应人数填入下面列联表;
记为“一般”,然后将骑手的对应人数填入下面列联表;
优秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根据(2)中的列联表,判断能否有![]() 的把握认为两种配送方案的效率有差异.
的把握认为两种配送方案的效率有差异.
附: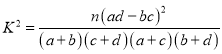 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
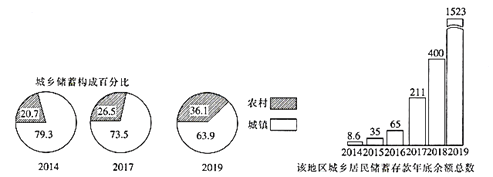
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
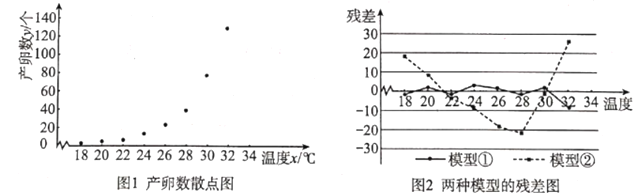
【题目】红铃虫(Pectinophora gossypiella)是棉花的主要害虫之一,其产卵数与温度有关.现收集到一只红铃虫的产卵数y(个)和温度x(℃)的8组观测数据,制成图1所示的散点图.现用两种模型①![]() ,②
,②![]() 分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
分别进行拟合,由此得到相应的回归方程并进行残差分析,进一步得到图2所示的残差图.
根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
|
25 | 2.89 | 646 | 168 | 422688 | 48.48 | 70308 |
表中![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(1)根据残差图,比较模型①、②的拟合效果,应选择哪个模型?并说明理由;
(2)根据(1)中所选择的模型,求出y关于x的回归方程(系数精确到0.01),并求温度为34℃时,产卵数y的预报值.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为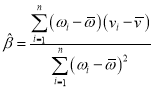 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com