
【题目】某北方村庄4个草莓基地,采用水培阳光栽培方式种植的草莓个大味美,一上市便成为消费者争相购买的对象.光照是影响草莓生长的关键因素,过去50年的资料显示,该村庄一年当中12个月份的月光照量X(小时)的频率分布直方图如下图所示(注:月光照量指的是当月阳光照射总时长).
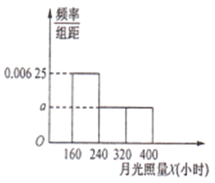
(1)求月光照量![]() (小时)的平均数和中位数;
(小时)的平均数和中位数;
(2)现准备按照月光照量来分层抽样,抽取一年中的4个月份来比较草莓的生长状况,问:应在月光照量![]() ,
,![]() ,
,![]() 的区间内各抽取多少个月份?
的区间内各抽取多少个月份?
(3)假设每年中最热的5,6,7,8,9,10月的月光照量![]() 是大于等于240小时,且6,7,8月的月光照量
是大于等于240小时,且6,7,8月的月光照量![]() 是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量
是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量![]() (小时)都不低于320的概率.
(小时)都不低于320的概率.
【答案】(1)平均数为![]() (小时);中位数为240(小时)(2)
(小时);中位数为240(小时)(2)![]() (3)
(3)![]()
【解析】
(1)利用各频率之和为1,计算出![]() ,然后根据频率分布直方图以及平均数,中位数的求法,可得结果.
,然后根据频率分布直方图以及平均数,中位数的求法,可得结果.
(2)根据月光照量![]() 、
、![]() 、
、![]() 的频率之比为
的频率之比为![]() ,结合分层抽样的方法,可得结果.
,结合分层抽样的方法,可得结果.
(3)采用列举法,将“6个月份之中随机抽取2个月份”所有情况列举出来,并计算“抽取到的2个月份的月光照量![]() (小时)都不低于320”的个数,结合古典概型可得结果.
(小时)都不低于320”的个数,结合古典概型可得结果.
(1)根据各频率之和为1,
则![]() ,
,
解得![]() .
.
月光照量![]() (小时)的平均数为
(小时)的平均数为
![]()
所以![]() (小时)
(小时)
设月光照量![]() (小时)的中位数为
(小时)的中位数为![]() ,
,
则![]() .根据中位数的定义,
.根据中位数的定义,
其左右两边的频率相等,都为0.5,可得
![]() ,
,
解得![]() .
.
所以月光照量![]() (小时)的中位数为240(小时).
(小时)的中位数为240(小时).
(2)因为月光照量![]() 、
、![]() 、
、
![]() 的频率之比为
的频率之比为![]() ,
,
所以若准备按照月光照量来分层抽样,
抽取一年中的4个月份来比较草莓的生长状况,
那么,抽取的月光照量![]() ,
,![]() ,
,
![]() 的月份数分别为
的月份数分别为
![]() .
.
(3)由题意,
月光照量![]() 的有5,9,10月,
的有5,9,10月,
月光照量![]() 的有6,7,8月,
的有6,7,8月,
故从该村庄2018年的5,6,7,8,9,10月份
之中随机抽取2个月份的月光照量![]() (小时)
(小时)
进行调查,所有的情况有:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() 共15种;
共15种;
其中,抽取到的2个月份的月光照量
![]() (小时)都不低于320的情况有:
(小时)都不低于320的情况有:
![]() 共3种;
共3种;
故所抽取到的2个月份的月光照量
![]() (小时)都不低于320的概率
(小时)都不低于320的概率![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数![]() ,
,![]() ,
,![]() .
.
(1)设![]() ,假设
,假设![]() 在
在![]() 上递减,求
上递减,求![]() 的取值范围;
的取值范围;
(2)假设![]() ,求证:
,求证:![]() .
.
(3)是否存在实数![]() ,使得
,使得![]() 恒成立,假设存在,求出
恒成立,假设存在,求出![]() 的取值范围,假设不存在,请说明理由.
的取值范围,假设不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴的建立极坐标系,曲线
轴正半轴为极轴的建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 与点
与点![]() 分别为曲线
分别为曲线![]() 动点,求
动点,求![]() 的最小值,并求此时的
的最小值,并求此时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为P1,P2,则( )
A. P1P2=![]() B. P1=P2=
B. P1=P2=![]() C. P1+P2=
C. P1+P2=![]() D. P1<P2
D. P1<P2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了减轻家庭困难的高中学生的经济负担,让更多的孩子接受良好的教育,国家施行高中生国家助学金政策,普通高中国家助学金平均资助标准为每生每年1500元,具体标准由各地结合实际在1000元至3000元范围内确定,可以分为两或三档.各学校积极响应政府号召,通过各种形式宣传国家助学金政策.为了解某高中学校对国家助学金政策的宣传情况,拟采用随机抽样的方法抽取部分学生进行采访调查.
(1)若该高中学校有2000名在校学生,编号分别为0001,0002,0003,…,2000,请用系统抽样的方法,设计一个从这2000名学生中抽取50名学生的方案.(写出必要的步骤)
(2)该校根据助学金政策将助学金分为3档,1档每年3000元,2档每年2000元,3档每年1000元,某班级共评定出3个1档,2个2档,1个3档,若从该班获得助学金的学生中选出2名写感想,求这2名同学不在同一档的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,线段
,线段![]() 、
、![]() 都是圆
都是圆![]() 的弦,且
的弦,且![]() 与
与![]() 垂直且相交于坐标原点
垂直且相交于坐标原点![]() ,如图所示,设△
,如图所示,设△![]() 的面积为
的面积为![]() ,设△
,设△![]() 的面积为
的面积为![]() .
.
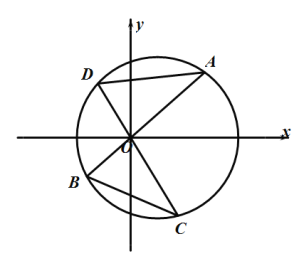
(1)设点![]() 的横坐标为
的横坐标为![]() ,用
,用![]() 表示
表示![]() ;
;
(2)求证:![]() 为定值;
为定值;
(3)用![]() 、
、![]() 、
、![]() 、
、![]() 表示出
表示出![]() ,试研究
,试研究![]() 是否有最小值,如果有,求出最小值,并写出此时直线
是否有最小值,如果有,求出最小值,并写出此时直线![]() 的方程;若没有最小值,请说明理由.
的方程;若没有最小值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为3的正方体ABCDA1B1C1D1中,A1E=CF=1.
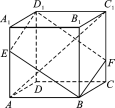
(1)求异面直线AC1与D1E所成角的余弦值;
(2)求直线AC1与平面BED1F所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com